3. Геометрический метод линейного программирования

Геометрическим методом ЛП можно решать лишь ограниченный класс задач ЛП.

Рассмотрим стандартную задачу ЛП с двумя переменными:

, (3.1)

, (3.2)

(3.3)

Каждое решение неравенства (3.1), (3.2) геометрически определяет полуплоскость с граничной прямой вида:

(3.4)

Для определения полуплоскости, соответствующей неравенству (3.1) необходимо вначале построить соответствующую граничную прямую (3.4). Затем взять любую точку, не лежащую на граничной прямой и подставить в неравенство (3.1). Если координаты этой точки удовлетворяют (3.1), то берется полуплоскость, содержащая эту точку. Если координаты этой точки не удовлетворяют (3.1), то берется полуплоскость, которая не содержит эту точку. Покажем на примере.

Пример. Определим полуплоскость, соответствующую неравенству . Вначале строим граничную прямую, которая задается уравнением:

.

График прямой представлен на рисунке (1).

Берем произвольную точку, не лежащую на этой прямой, например, точку с координатами (0,0). Подставляем координаты в исходное неравенство:

. Это неравенство удовлетворяется и, следовательно, берем полуплоскость, содержащую точку (0,0). Для удобства ставим штриховку в сторону этой точки.

Рис. 1.

Определение 3.1. Множество называется выпуклым, если оно вместе с любыми своими двумя точками содержит отрезок, соединяющий эти точки.

Полуплоскость является выпуклым множеством. Пересечение всех выпуклых множеств является выпуклым множеством.

Если система неравенств (3.1), (3.2) совместна, то область её решений является выпуклым многоугольником.

Согласно основной теореме линейного программирования, если задача ЛП имеет решение, то целевая функция достигает оптимального значения хотя бы в одной угловой точке многоугольника решений. Если же целевая функция достигает оптимального значения более, чем в одной угловой точке, то она достигает того же самого решения в любой точке отрезка, соединяющего эти точки.

Согласно этой теореме, экстремум целевой функции необходимо искать либо в угловой точке, либо на стороне многоугольника решений. Для этого необходимо вначале построить градиент функции F, т. е. вектор:

Направление вектора градиента показывает направление возрастания функции, соответственно, обратное направление показывает направление убывания функции.

Затем нам необходимо построить линию уровня функции F, т.е. прямую перпендикулярную градиенту и задаваемую уравнением: c₁x₁+c₂x₂=const.

Передвигая указанную линию перпендикулярно вектору градиента мы можем получить один из следующих случаев.

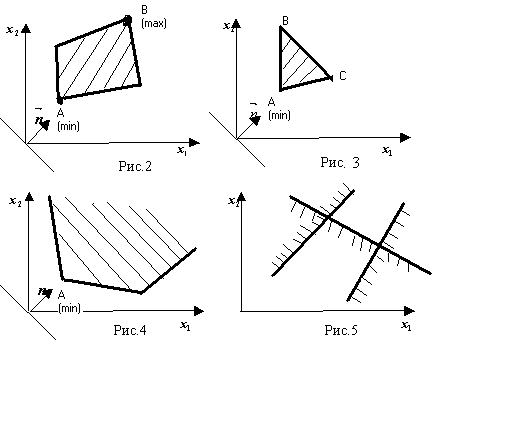
1. Случай единственного решения (рис. 2)

В этом случае точка А есть точка минимума, а точка В есть точка максимума (если бы, например, вектор был направлен в противоположную сторону, то в этом случае точка В была бы точкой минимума, а точка А – точкой максимума).

2. Случай бесконечного множества решений (рис. 3)

На рисунке 3 линия уровня целевой функции параллельна стороне ВС. Такой случай возникает только тогда, когда коэффициенты в целевой функции будут пропорциональны коэффициентам в некотором неравенстве , т. е. существует число , такое, что .

В этом случае точка А есть точка минимума, а максимум целевой функции доставляют все точки отрезка BC.

3. Случай неограниченности целевой функции (рис. 4)

Точка А есть точка минимума, а точки максимума не существует.

4. Случай несовместности (3.1), (3.2). (рис. 5)

В этом случае решение задачи отсутствует, т. к. нет ни одной общей точки, удовлетворяющей сразу всем неравенствам (3.1), (3.2).

Алгоритм геометрического метода ЛП

1. Строят прямые (3.4), и определяют полуплоскости (3.1) и (3.2). При этом необходимо учесть, что в силу условий (3.2), рисунок должен всегда находиться в первой координатной четверти, т. е. не заходить за начало координат ни левее, ни ниже. Затем определяют многоугольник решений. Если получили случай, представленный на рис. 5, то решений нет.

2. Строят градиент целевой функции, а именно вектор . Строят перпендикулярную градиенту линию уровня целевой функции, проходящую через начало координат .

Передвигаем линию уровня вдоль градиента параллельно самой себе и визуально определяем точки экстремума.

3. Определяют координаты точки максимума (минимума) целевой функции. Для этого решают систему уравнений прямых, точками пересечения которых является точка максимума (минимума). Затем подставляют координаты этих точек в целевую функцию и находят значение функции в этих точках.

Пример. Найдем наибольшее и наименьшее значения целевой функции F при заданных ограничениях:

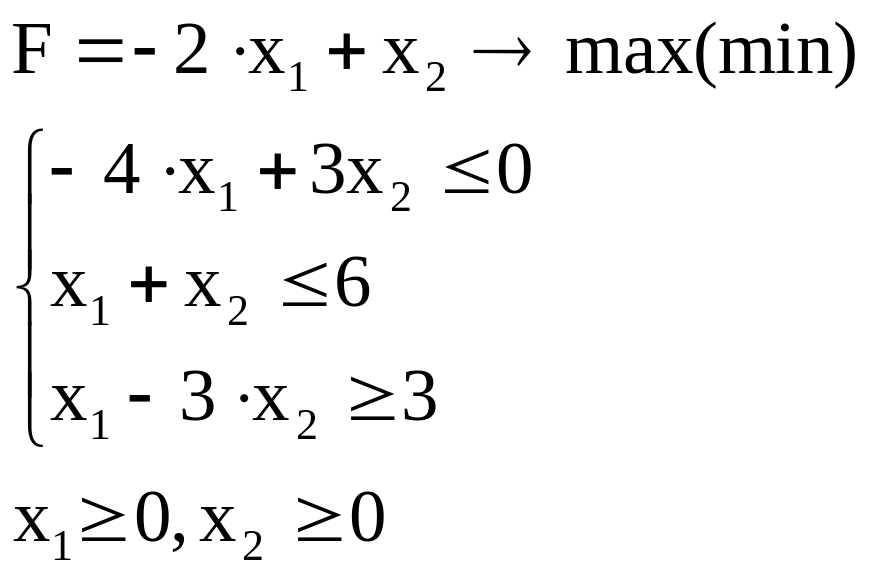
Строим прямые (3.4), уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств:

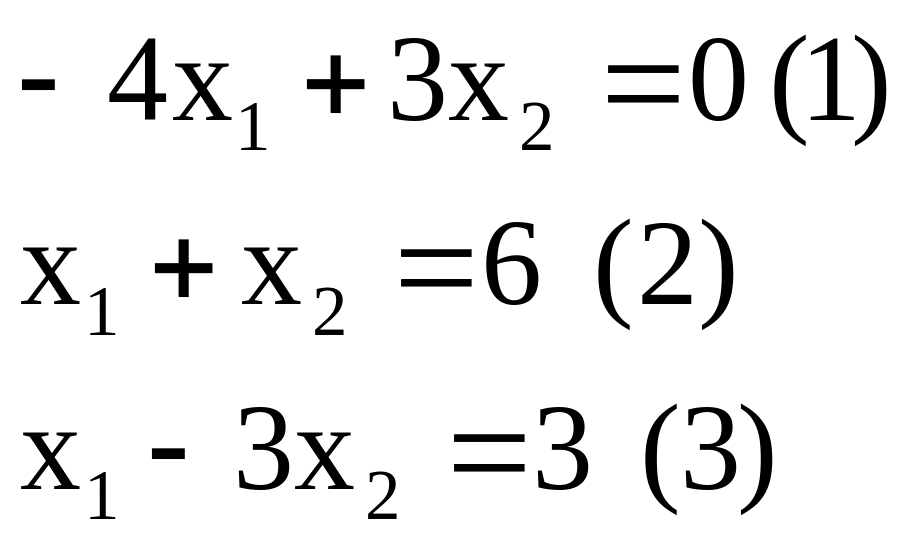
Определяем полуплоскость, соответствующие исходным неравенствам. В результате пересечения всех полуплоскостей находим многоугольник решений. Это будет треугольник ABC.

Построим градиент целевой функции и перпендикулярную ему прямую. Передвигая линию уровня вдоль градиента и перпендикулярно градиенту, находим, что максимум достигается в точке А, а минимум в точке В.

Рис.6.

Определим координаты точек максимума и минимума целевой функции и вычислим значения функции в найденных точках.

Точка максимума лежит на пересечении прямой (3) и горизонтальной осью системы координат, которая задается уравнением :

Точка минимума лежит на пересечении прямой (2) и горизонтальной осью системы координат:

Подставляем координаты найденных точек в целевую функцию. Минимальное значение целевой функции

.

Максимальное значение целевой функции

.