1. Основные законы линейных электрических цепей:

Закон Ома

В настоящее время под законом Ома понимают все соотношения,связывающие между собой напряжение и ток. I = GU , G – проводимость, величина, обратная сопротивлению.

Первый закон.

Узел – это точка в схеме, где сходятся не менее трех ветвей. При использовании ЭВМ для ввода исходных данных узлами выделяют каждый элемент схемы замещения.Эти узлы называют ложными или устранимыми. В дальнейшем речь будет идти о неустранимых узлах. Алгебраическая сумма токов в узле равна нулю. Поэтому число независимых уравнений по первому закону Кирхгофа равно

N y −1, где Ny – число узлов цепи.

Второй закон Кирхгофа относится к контуру. Алгебраическая сумма напряжений на приемниках в любом контуре равна алгебраической сумме ЭДС, действующих в этом же контуре.

Баланс мощностей – это интерпретация закона сохранения энергии в электротехнике.

Мощность генераторов энергии в электрической цепи равна мощности потребителей: Pг=Рн , причем 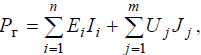Эти суммы алгебраические. Источник может как вырабатывать, так ипотреблять (заряд аккумулятора) электрическую энергию.Если направления ЭДС и тока через источник ЭДС совпадают, мощность источника записывают в уравнении баланса мощностей с положительным знаком. Он работает в режиме генератора.При противоположных направлениях ЭДС и тока мощность в уравнении баланса учитывают с отрицательным знаком (режим потребителя).

2. Расчет токов методом непосредственного использования законов Кирхгофа.

Предварительно нужно выявить в схеме узлы и ветви. Ветвь – участокс одним током между двумя узлами. В схеме столько токов, сколько ветвей.Направления их указывают произвольно.Число уравнений должно быть минимальным, но достаточным и равным числу неизвестных токов, т. е. m − mJ , где m – общее число ветвей в схеме; mJ – число ветвей с источниками тока.По первому закону Кирхгофа составляют n −1 уравнение, где n – число узлов схемы. В этих уравнениях учитывают и токи источников тока. При

подготовке данных для ввода в ЭВМ известные величины записывают справа

от знака равенства. Поэтому первый закон Кирхгофа формулируют следующим образом:

ΣI = ΣJ ,где Σ I – алгебраическая сумма неизвестных токов ветвей в узле; Σ J – алгебраическая сумма токов источников тока, присоединенных к этому же узлу. Недостающие уравнения дописывают по второму закону Кирхгофа.Уравнения по второму закону Кирхгофа составляют для контуров, не содержащих источников тока. Систему уравнений по законам Кирхгофа можно записать в матричной

форме следующим образом: [a]⋅[I] = [F],где [a] – квадратная матрица коэффициентов;

[I ] – матрица-столбец неизвестных токов ветвей;[F] – матрица-столбец активных параметров, которыми являются токи источников тока и ЭДС.

Уравнения в системе не однотипны, так как записаны на основании двух

разных законов. В уравнениях по первому закону Кирхгофа коэффициенты aij безразмерны и могут принимать значения ±1 или 0. В правой части Fj = ΣJ . В уравнениях по второму закону Кирхгофа коэффициенты aij имеют размерность сопротивления, Fi = ΣE . Если j – ветвь входит в i -й контур,для которого составлено уравнение, то aij = ±Rij не входит, aij =0 .