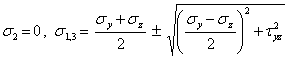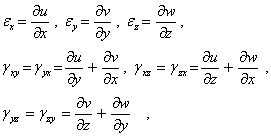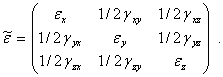Лекции по Сопромату. Подробный и полнейший конспект лекций по сопротивлению материалов / 7

Лекция № 7. Плоское напряженное состояние

   Рассмотрим важный для приложений случай плоского напряженного состояния, реализуемого, например, в плоскости Oyz. Тензор напряжений в этом случае имеет вид

   Геометрическая иллюстрация представлена на рис.1. При этом площадки х=const являются главными с соответствующими нулевыми главными напряжениями. Инварианты тензора напряжений равны , а характеристическое уравнение принимает вид

Корни этого уравнения равны

(1)

Нумерация корней произведена для случая

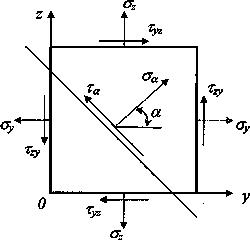Рис.1. Исходное плоское напряженное состояние.

 

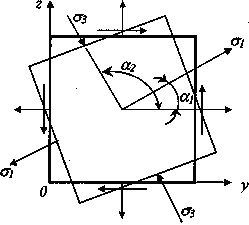Рис.2. Позиция главных напряжений

 

   Произвольная площадка характеризуется углом на рис. 1, при этом вектор п имеет компоненты: , , n_х=0. Нормальное и касательное напряжения на наклонной площадке выражаются через угол следующим образом:

	(2)
	(3)

   Так как на главных площадках касательное напряжение отсутствует, то, приравнивая нулю выражение (3), получим уравнение для определения угла между нормалью п и осью Оу

(4)

   Наименьший положительный корень уравнения (4) обозначим через . Так как tg(х)—периодическая функция с периодом , то имеем два взаимно ортогональных направления, составляющие углы и с осью Оу. Эти направления соответствуют взаимно перпендикулярным главным площадкам (рис. 2).

   Если продифференцировать соотношение (2) по и приравнять производную нулю, то придем к уравнению (4), что доказывает экстремальность главных напряжений.

   Для нахождения ориентации площадок с экстремальными касательными напряжениями приравняем нулю производную от выражения

,

откуда получим

(5)

 

Сравнивая соотношения (4) и (5), находим, что

   Это равенство возможно, если углы и отличаются на угол . Следовательно, направления площадок с экстремальными касательными напряжениями отличаются от направлений главных площадок на угол (рис. 3).

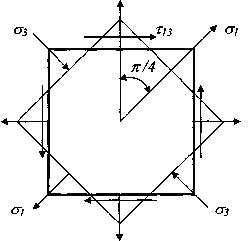Рис.3. Экстремальность касательных напряжений

 

Величины экстремальных касательных напряжений получим после подстановки (5) в соотношение (3) с использованием формул

.

После некоторых преобразований получим

Сравнивая это выражение с полученными ранее значениями главных напряжений (2.21), выразим экстремальные касательные напряжения через главные напряжения

Аналогичная подстановка в (2) приводит к выражению для нормальных напряжений на площадках с

Полученные соотношения позволяют проводить направленно-ориентированный расчет конструкций на прочность в случае плоского напряженного состояния.

 

ТЕНЗОР ДЕФОРМАЦИИ

   Рассмотрим вначале случай плоской деформации (рис. 4). Пусть плоский элемент MNPQ перемещается в пределах плоскости и деформируется (изменяет форму и размеры). Координаты точек элемента до и после деформации отмечены на рисунке.

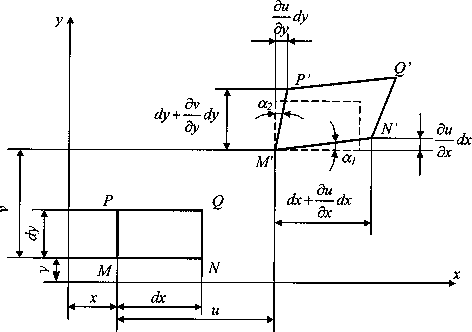Рис.4. Плоская деформация.

 

По определению относительная линейная деформация в точке М в направлении оси Ох равна

Из рис. 4 следует

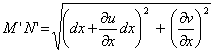
Учитывая, что MN=dx, получим

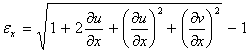
В случае малых деформаций, когда , , можно пренебречь квадратичными слагаемыми. С учетом приближенного соотношения

справедливого при x<<1, окончательно для малой деформации получим

Угловая деформация определяется как сумма углов и (4). В случае малых деформаций

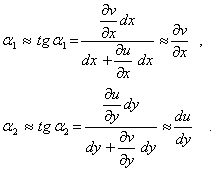
Для угловой деформации имеем

Проводя аналогичные выкладки в общем случае трехмерной деформации, имеем девять соотношений

(6)

   связывающих линейные и угловые деформации с перемещениями. Эти соотношения носят название соотношений Коши.

Три линейных и шесть угловых деформаций (6) образуют тензор малых деформаций

(7)

   Этот тензор полностью определяет деформированное состояние твердого тела. Он обладает теми же свойствами, что и тензор напряжений. Свойство симметрии непосредственно следует из определения угловых деформаций. Главные значения и главные направления, а также экстремальные значения угловых деформаций и соответствующие им направления находятся теми же методами, что и для тензора напряжений.

   Инварианты тензора деформаций определяются аналогичными формулами, причем первый инвариант тензора малых деформаций имеет ясный физический смысл. До деформации его объем равен dV₀ =dxdydz. Если пренебречь деформациями сдвига, которые изменяют форму, а не объем, то после деформации ребра будут иметь размеры

(рис. 4), а его объем будет равен

.

Относительное изменение объема

в пределах малых деформаций составит

что совпадает с определением первого инварианта. Очевидно, что изменение объема есть физическая величина, не зависящая от выбора системы координат.

   Так же, как и тензор напряжений, тензор деформаций можно разложить на шаровой тензор и девиатор. При этом первый инвариант девиатора равен нулю, т. е. девиатор характеризует деформацию тела без изменения его объема.