2. Пример применения метода Ритца

Требуется найти приближённое решение задачи о минимуме функционала

, (1)

y(0) = 0, y(1) = 0 (2)

и сравнить с точным решением.

Пусть (k = 1, 2, …) – система координатных функций.

Функции φ_k(x), очевидно, удовлетворяют краевым условиям φ_k(0) = 0, φ_k(1) = 0, являются линейно независимыми и представляют в пространстве C₁[0,1] полную систему.

При k = 1 получаем y₁(x) = α₁(x-x²). Подставляя это выражение для y₁(x) в функционал (1), получим

Коэффициент α₁ находим из уравнения

,

откуда . Следовательно,

.

Рассмотрим точное решение. Уравнение Эйлера для данного функционала:

.

Решая это неоднородное линейное уравнение, находим

.

Используя граничные условия y(0) = 0, y(1) = 0, получим окончательно:

.

В результате сравнения точного решения с приближённым получаем:

x	Точное решение y0(x)	Приближенное решение y1(x)	Невязки |y1(x)-y0(x)|
0,00	0	0	0
0,25	-0,044	-0,052	0,008
0,50	-0,070	-0,069	0,001
0,75	-0,060	-0,052	0,008
1,00	0	0	0

δ₁ = 0.008,

где незязка δ₁ = max| y₁(x_i) - y₀(x_i) |

3.Отыскание последовательности итераций по методу Ритца(n=1,2,3,4,5)

C помощью Mathcad 15.

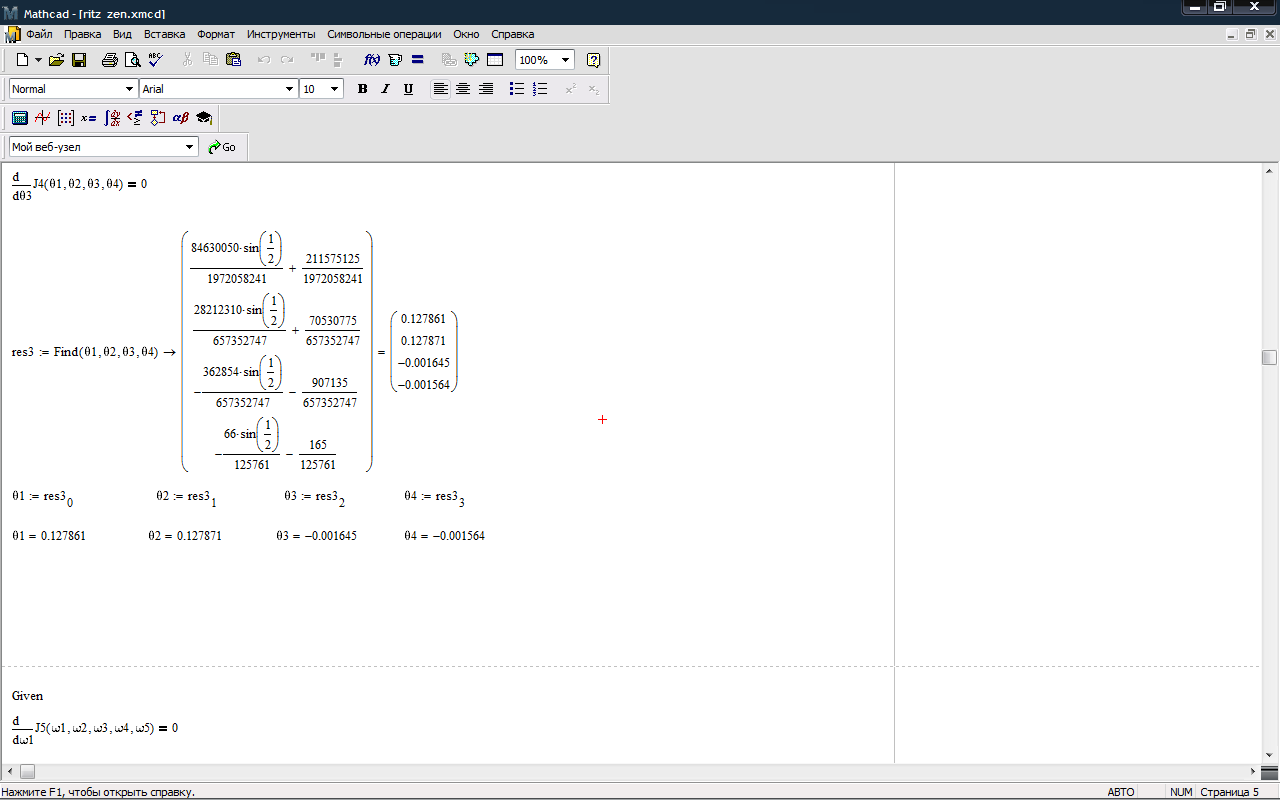
yφ5(x):=y5(x,ω1,ω2,ω3,ω4,ω5) →x(sin(1/2)+2) - 0.127861585917x(1-x)-0.127860095521x²(1-x)+0.001600242723x³(1-x)+0.001630189340x⁴(1-x)-0.000033285979x⁵(1-x)

4.Невязки. Графики приближений. Mathcad 15.

(продолжение программы из 4 пункта).

Вычислим невязки: δ_n = max| y_n(x_i) - y₀(x_i) |

Δ_n = max| y_n+1(x_i) - y_n(x_i) |)

Задание шага:

Вычисление:

n=1

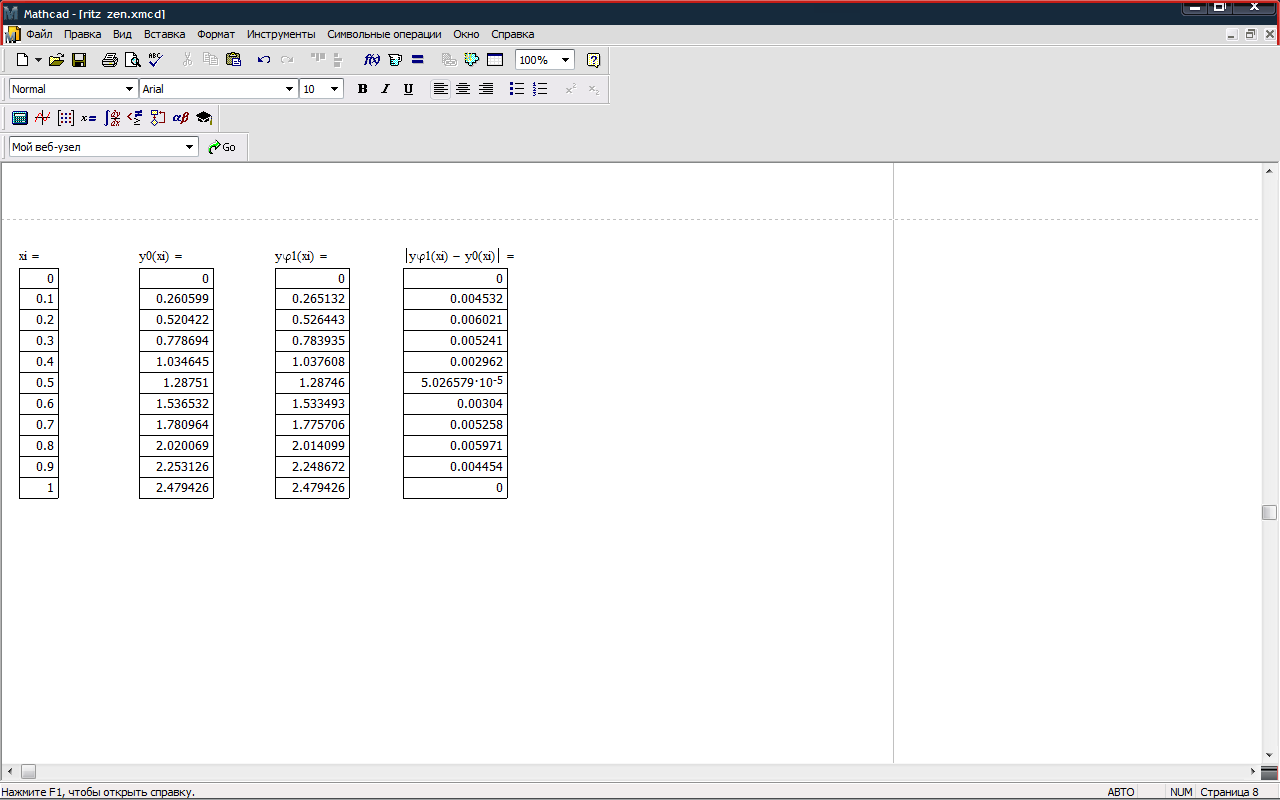
δ₁=0.006021

n=2

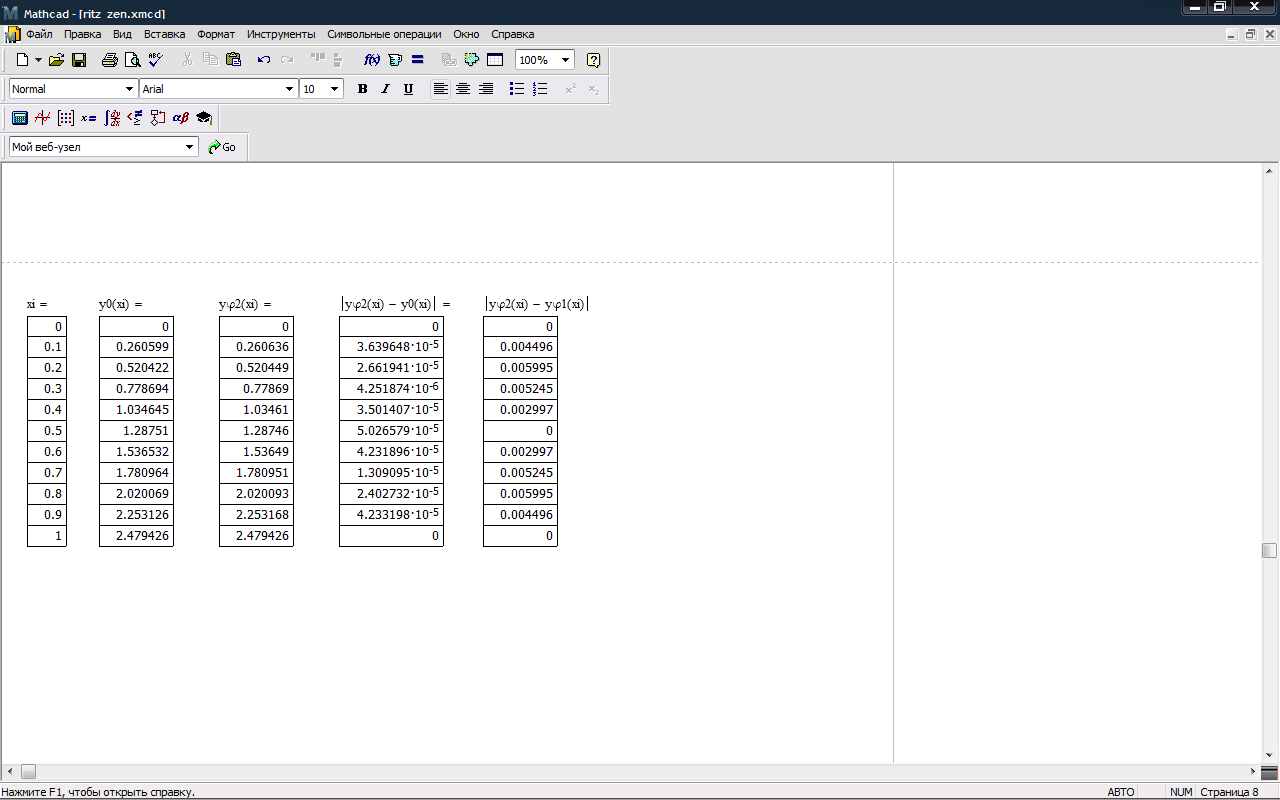
δ₂ = 5.026579*10^-5

Δ₁= 0.005995

n=3

δ ₃ =4.434153*10^-6

Δ₂=5.024098*10^-5

n=4

δ ₄=2.480472*10^-8

Δ₃=4.418764*10^-6

n=5

δ ₅=1.632083*10^-9

Δ₄=2.479794*10^-8

Как показывают расчёты, с ростом n невязки стремятся к нулю.

Так как графики приближения и точного решения слились, выполним их в искаженном масштабе.

6.Результаты работы

В результате проделанной работы, мы получили следующие приближённые решения:

Первое: yφ1(x):=y1(x,α1)→2.008726535498x-0.190988816577x(1-x)

Второе: yφ2(x):=y2(x,β1,β2)→2.008726535498x-0.128545766366x(1-x)- -0.124886100420x²(1-x)

Третье: yφ3(x):=y3(x,µ1,µ2,µ3)→ 2.008726535498x-0.127749218404x(1-x)- -0.128876148013x²(1- x)+0.003990047593x³(1-x)

Четвертое: yφ4(x):=y4(x,θ1,θ2,θ3,θ4)→ 2.008726535498x-0.127860793895x(1-x)- -0.127871188339x²(1-x)+0.001644621520x³(1-x)+0.001563617381x⁴(1-x)

Пятое: yφ5(x):=y5(x,ω1,ω2,ω3,ω4,ω5) →2.008726535498x-0.127861585917x(1-x)-0.127860095521x²(1-x)+0.001600242723x³(1-x)+0.001630189340x⁴(1-x)-0.000033285979x⁵(1-x)

В результате их сравнения были получены следующие невязки:

δ₁=0.006021

δ₂ = 5.026579*10^-5

δ ₃ =4.434153*10^-6

δ ₄=2.480472*10^-8

δ ₅=1.632083*10^-9

(отличия от точного решения)

Δ₁= 0.005995

Δ₂=5.024098*10^-5

Δ₃=4.418764*10^-6

Δ₄=2.479794*10^-8

(отличия приближений друг от друга)

Сделаем вывод, что с ростом n невязки стремятся к нулю, т.е. приближения стремятся к точному решению задачи.