Алгоритм решения задач динамического программирования.

Определяем все состояния системы при переходе из начального состояния в конечное состояние . На каждом шаге целевые функции имеют вид: и определено уравнение состояния: Из уравнения Беллмана для по находим оптимальное управление на ом шаге По и определяем состояние системы после го шага: Из уравнения Беллмана для находим оптимальное управление на ом шаге По и определяем состояние системы после го шага: и так далее. Условно этот процесс можно представить в виде:

Задача. Инвестиционная компания планирует вложить средства в четыре проекта. Полная сумма инвестиций составляет 6 млн. рублей. В таблице приведена прогнозируемая доходность проектов для различных объектов инвестиций. Требуется найти наилучший вариант инвестиций, при котором суммарный доход будет максимальным. Предполагается, что прибыльность проектов не зависит от вложений в другие проекты.

Размер инвестиций	Доходность проектов
	1-ый проект	2-ой проект	3-ий проект	4-ый проект
1	6	5	3	4
2	10	9	6	7
3	12	11	11	12
4	16	13	17	15
5	20	16	19	18
6	22	18	13	21

Решение. Целевой функцией задачи является результирующий доход , при условии где - функции дохода го проекта при вложении средств. Зависимость этих функций от объёмов вложений приведены в таблице

Объёмы вложений
0	0		0	0		0
1	6		5	3		4
2	10		9	6		7
3	12		11	11		12
4	16		13	17		15
5	20		16	19		18
6	22		18	13		21

С учётом постановки данную задачу динамического программирования можно разбить на 4 этапа. Каждый этап характеризуется выбором инвестиций в какой то конкретный проект при учёте оптимальных вложений на предыдущих шагах. Математически подобная процедура пошагового выбора имеет вид:

Следовательно, динамическое программирование начинается с первого шага, на котором средства инвестируются в первый проект, и завершается четвёртым шагом, при котором вложения идут в четвёртый проект. Параметр в рекуррентных соотношениях меняется от 0 до 6. Функция , в силу первого из равенств, совпадает с функцией дохода первого проекта и её значения заданы следующей таблицей

	0	1	2	3	4	5	6
	0	6	10	12	16	20	22

Значения функции находим, используя рекуррентное соотношение 2):

1.

2.

3.

4.

5.

6.

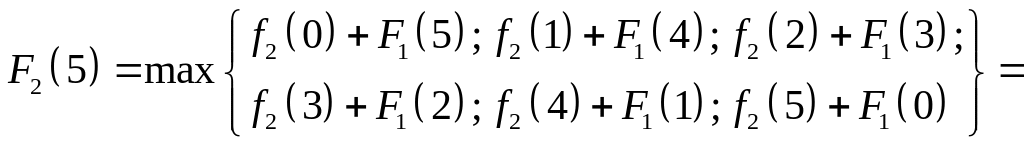
7.

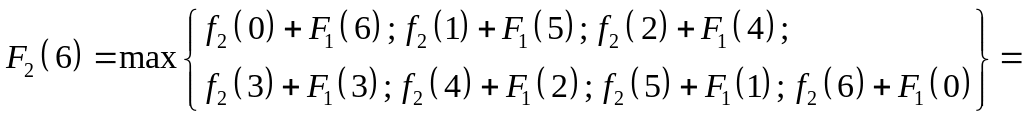
Сведём полученные данные для функции в таблицу

	0	1	2	3	4	5	6
	0	6	11	15	19	21	25

Аналогично, используя рекуррентные соотношения 3) и 4) соответственно, находим значения функций . Запишем данные в таблицу

	0	1	2	3	4	5	6
	0	6	11	15	19	23	28
	0	6	11	15	19	23	28

Максимум целевой функции , равный 28, складывается из расчета:

Таким образом, оптимальный план распределения инвестиций имеет вид:

млн. руб.; млн. руб.; млн. руб.