Задача Поиск оптимального объема производства в условиях неопределенности

АО «Силуэт» выпускает женскую одежду, которая реализуется через сеть фирменных магазинов. Сбыт продукции во многом зависит от состояния погоды (теплая, холодная). АО «Силуэт» занимается производством женской одежды двух видов: платья и костюмы. Затраты на производство и реализацию единицы продукции составляют: костюмы – 270 руб., платья – 80 руб., а продажная цена – 480 и 160 руб. По данным наблюдений – АО может реализовать в течение мая в условиях теплой погоды 1200 костюмов и 3950 платьев, а при холодной погоде 2000 костюмов и 1250 платьев.

Задача состоит в максимизации средней величины прибыли от реализации выпущенной продукции с учетом капризов погоды. АО располагает в этих ситуациях двумя стратегиями: в расчете на теплую погоду (стратегия А); в расчете на холодную погоду (стратегия В).

Если АО примет стратегию А и погода будет теплой (стратегия природы С), то вся продукция будет реализована, значит, АО получит прибыль от реализации П(АС):

П(АС) руб.

Если АО примет стратегию А и погода будет холодной (стратегия природы Д), то костюмы будут проданы полностью. А платья – только в количестве 1250 шт. Прибыль АО в данном случае П(АД) составит:

П(АД) руб.

Аналогичным образом можно определить прибыль предприятия в случае применения им стратегии В. В условиях теплой погоды (стратегия природы С) прибыль П(ВС) составит:

П(ВС) руб.

Принятие той стратегии, но в условиях холодной погоды, позволит реализовать всю выпущенную продукцию, и прибыль П(ВД) в этом случае составит:

П(ВД) руб.

Рассматривая АО «Силуэт» и природу в качестве двух игроков Р1 и Р2, получим по итогам произведенных расчетов так называемую платежную матрицу следующего вида:

Игроки	Р1 (АО «Силуэт»)
Р2 (природа)	стратегии	А	В	max по строкам
	С	568000	136000	136000
	Д	136000	520000	136000
	max по столбцам	568000	520000

По данным платежной матрицы игрок Р₁ (АО «Силуэт») никогда не получит прибыль меньше 136000 руб. Если погодные условия совпадут с выбранной стратегией, то прибыль АО (выигрыш) будет составлять 568000 или 520000 руб. Если игрок Р₁ будет постоянно принимать стратегию А, а игрок Р₂ – стратегию Д, то прибыль снизится до 136000 руб. о же самое будет, если игрок Р₁ постоянно принимает стратегию В, а игрок Р₂ – стратегию С. Следовательно, АО может обеспечить себе наибольшую прибыль, если будет попеременно принимать то стратегию А, то стратегию В. Такая стратегия называется смешанной. А ее элементы (А и В) – чистыми стратегиями.

Оптимизация смешанной стратегии позволит игроку Р₁ всегда получать среднее значение выигрыша (прибыли) независимо от стратегии игрока Р₂. Для оптимизации смешанной стратегии необходимо определить частоту применения игроком Р₁ стратегии А и стратегии В. Обозначим частоту применения стратегии А через х, тогда частота применения стратегии В будет (1-х).

Если игрок Р₁ принимает оптимальную смешанную стратегию, то и при стратегии игрока Р₂ (природа) С (теплая погода) и при его стратегии Д (холодная погода) игрок Р₁ должен получить одинаковую среднюю прибыль (выигрыш):

;

;

.

Действительно, игрок Р₁, принимая чистые стратегии А и В в соотношении , будет иметь оптимальную смешанную стратегию, при которой средний выигрыш будет составлять:

1) при теплой погоде (стратегия С игрока Р₂)

П(С)= руб.;

2) при холодной погоде (стратегия Д игрока Р2)

П(Д)= руб.

Таким образом, средняя прибыль (средний платеж), которую получит АО «Силуэт» при реализации оптимальной смешанной стратегии, будет равна 339300 руб. Средний платеж, который получается при реализации оптимальной смешанной стратегии, называется ценой игры.

В заключение следует определить, сколько платьев и костюмов должно выпустить в мае АО «Силуэт» для реализации оптимальной смешанной стратегии, т. е. для получения максимальной прибыли при любой погоде (использовать округление результата до меньшего целого значения):

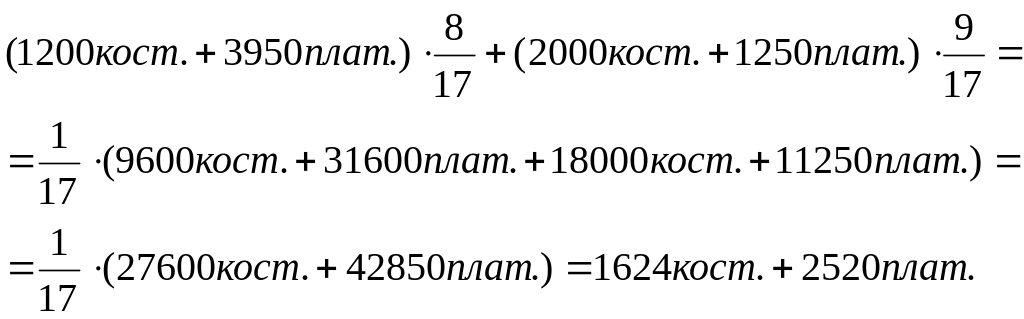
Значит, оптимальная стратегия АО «Силуэт» означает выпуск 1624 костюмов и 2520 платьев, в этом случае при любых погодных условиях АО получит прибыль = 339300 руб., а при теплой погоде (стратегия С игрока Р₂)

= руб.;

= руб.

За счет округления числа костюмов и платьев могут получиться разные значения (оба значения должны быть близки к рассчитанному ранее среднему значению прибыли). В этом случае в качестве гарантированной средней прибыли надо выбрать наименьшее из двух значений.