2.2.2 Моделирование нормально распределенных случайных величин

В технике и природе наиболее распространенное распределение случайных чисел – гауссовское или нормальное.

Нормальной (или гауссовской) называется случайная величина X, определенная на всей числовой оси (− ∞, ∞) имеющая плотность распределения вероятности:

.

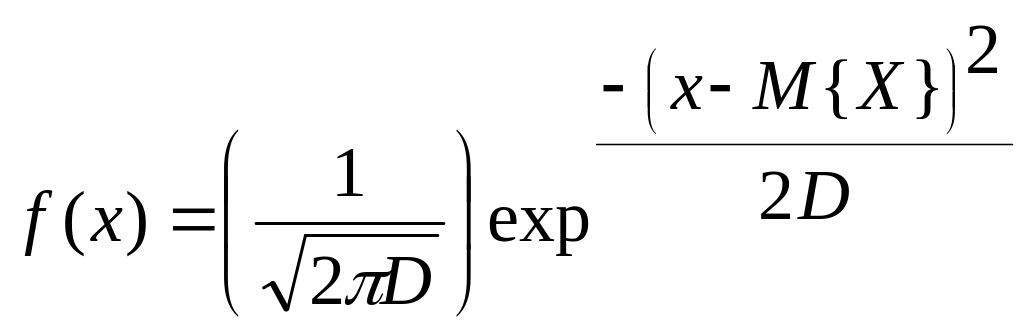Здесь D=σ² – дисперсия случайной величины, а M{X} – математическое ожидание случайной величины X.

Распространенный алгоритм моделирования таких величин основан на центральной предельной теореме теории вероятностей.

Р ассмотрим алгоритм моделирования нормально распределенных случайных величин.

Известно, что если случайная величина X распределена равномерно в интервале (0;1), то ее математическое ожидание М(X)=1/2, а дисперсия D(X) = 1/12.

Для практического использования можно считать, что случайная величина распределена нормально при n ≥ 8 (n – количество случайных величин) с математическим ожиданием M{X}=n/2, дисперсией D{X}=n/12 и среднеквадратичным отклонением σ= = .

Величина М(X) характеризует центр тяжести распределения X и не влияет на форму кривой. Величина σ же характеризует разброс случайной величины X относительно ее среднего значения М(X) (см. рисунок 3).

Так как моделирование любого нормального распределения с параметрами (M{X}, σ) может быть осуществлено по очевидной формуле X= M{X}+σ∙R, где R={r₁, r₂, …, r_n}− сгенерированная в интервале [0;1) случайная величина, то нормально распределенные случайные величины с параметрами (0;1) можно вычислять по следующей приближенной формуле:

.

При n = 12 эта формула заметно упрощается: .

Пример 3.

1. Разыграть 100 возможных значений случайной величины Х распределенной нормально с параметрами M{X} = 0 и σ = 1.

2. Оценить параметры разыгранной случайной величины Х.

Решение:

1. Выберем 12 случайных чисел распределенных равномерно в интервале (0;1) из таблицы случайных чисел, либо из компьютера. Сложим эти числа и из суммы вычтем 6, в итоге получим:

X₁= R = = (0,10+0,09+…+0,67)-6=-0,99.

Поступая аналогичным образом, найдем остальные возможные значения X₂, X₃, …, X₁₀₀.

2. Выполнив необходимые расчеты, найдем выборочную среднюю, которая является оценкой M{X} и выборочное среднее квадратичное отклонение (выборочная дисперсия), которое является оценкой σ.

Выборочное среднее: .

Выборочная дисперсия: .

Величина называется выборочным средним, − выборочной дисперсией случайной величины X. Значения и можно принять в качестве оценок математического ожидания M{X} и дисперсии D{X} величины X, т.е. , . Приближенные равенства становятся точными в пределе, когда n→. Выборочное среднеквадратичное отклонение σ_n равно корню квадратному из выборочной дисперсии .

Получим:

_.

Как видим, оценки удовлетворительны, т.е. близко к нулю, а близко к единице.

Если требуется разыграть значения нормальной ненормированной случайной величины с математическим ожиданием M{X} отличным от нуля и σ отличным от единицы, то сначала разыгрывают возможные значения r_i нормированной случайной величины в интервале [0;1), а затем находят искомое значение по формуле

X_i= M{X}+σ∙r_i,

которая получена из соотношения: .