10 Вероятностные оценки случ велич и построение гистограммы распределения случ величин

Для нахождения вероятностных оценок весь объем выборки случ велич разбивают на несколько равных интервалов (5-10)

Также сущ империч зависимость для определения более точных интервалов

К=3,3lg(n)+1

n-это объем выборки

Далее определ длину равных интервалов -это отношение размаха к кол-ву интервалов. . Потом все оформляем в таблицу.

-начало первого интервала

-конец интервала

-частота или число случ велич попавших в каждый интервал

-частность

Строится график…………

11 Имперические функции вероятности отказа и вероятн безотказной работы

На основе полученных данных об опытном распределении вероятности отказа и вероятности безотказной работы строятся графики этих функций

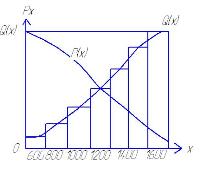
Имея значение вероятностного отказа и безотказной работы можно решить практические задачи по определению периодичности технического обслуживания изделия

12 Нормальный закон распределения случайных величин

З-н Гауса

Этот закон хорошо описывает распределение случ велич на изменение кот влияет большое число факторов равнознач по величине. Нормальному з-ну близко распределение значений наработки до отказа большинства изнашивающих деталей машин

Интегральная ф-я для нормального з-на распредел опред по след зависимости

х-значение случ велич

-математ ожидание случ велич

е- основание натур логарифма

Ф-я плотности наход по след зависимости

Графически кривая распредел для нормального закона выглядит след образом

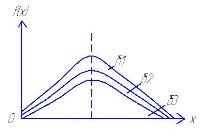
Для упрощения практич вычислений была введена величина наз интегралом вероятности

-кванти распредел

13 Нормальный логарифмический з-н распред случ велич.

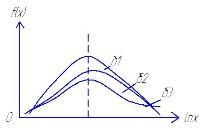
При логарифмич законе логарифмы значений случ велич подчиняются нормальному закону распредел. Плотность распредел для норм логарифм закона определ

,

- пар-ры распредел

14 Экспоненциальный з-н распред случ велич

Это з-н хорошо описывает распредел случ велич изменение кот обусловлено каким либо одним доминирующ фактором. Данный закон описыв распред внезапных отказов и применяется для описания наработки сложных систем. Функция плотности для экспоненц з-на находится :

Математич ожидание случ велич подчиняющ экспоненц закону совпадает со средним квадратичным отклонением и связ с паламетром след образом:

Кривая плотности экспоненц зак выглядит след образом:

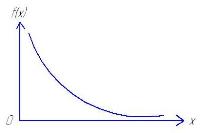
15 Распределение вейбула случ величины

Данное распред явл наиболее общим распредел времени безотказной работы элементов машин до предельного состояния. Это распред использ при описании наработки деталей при установленных разрушений.

Опред след образом: a,m- параметры распред. Значение параметра m зависит от коэфф вариации и определ расчетом табличн данными или графоаналитическим методом. В зависимости от этого параметра кривая плотности распред изменяет свою форму в широком диапазоне.

16 Проверка гипотезы о законе распред случ величины

При исследовании надежность машин и их элементов после предворит анализа исходных данных выдвигают предположение о виде закона распред в значении показателя надежности. Учитывается значение коэфф вариации и вид гистограммы распределения.

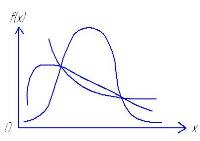
Пр. <0,33-нормальн з-н распредел

1-экспоненц з-н распределения

>0,33- расперел Вейбула

Выдвинутую гипотезу о распред случ величины проверяют по результатам статистической обработки