7 Виды закономерности изменения технического состояния сдкм.

Все процессы в природе и технике в том числе в области СДКМ могут быть двух видов:

1это процессы характерные функциональными зависимостями.

2случайные (вероятностные) процессы

Для функциональных процессов характерны жесткая связь м.д функцией (зависимой переменной) и аргументом (не зависим переменной) когда определенному значению аргумента соотв опред знач функции.

Случайные процессы происходят под действием многих факторов значение кот часто неизвестно поэтому результат вероятностного процесса могут принимать различн кол-ые значения и наз случ величинами.

Случайный процесс может быть представлен функцией кот при каждом новом значении аргумента хар-ся набором нескольких случайных величин.Конкретные знач случ функции при фиксированном значении аргумента наз реализацией случ величины

Закономерности изменения технич сост машины по ее наработке (законом первого вида). Хар-ют процесс изменения технич сост объекта в зависимости от ее наработке.Эти закомом у многих изделий мех-ов или деталей носят плавный монотонный характер приводящ к возникнов так наз постоянных отказов

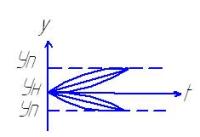
Проведенные исследования показывают, что в случае постепенных отказов изменение параметра технич сост изделия аналитич может быть описана 2мя видами функций

1Целой рациональной функцией n-го порядка

2Степенная функция где - это нач знач параметра технич сост.

, , , - коэфф определ характер и степень зависимости

Закономерности вариации случ-х величин(законом 2го вида)

Зак 2го вида хар-ют вариацию значений параметров технич сост или наработку до предельного состояния.

Применит к технич состоянию однотипных изделий причинами вариации явл:

1даже не значит изменение от изделия к изделию качество обработки материала, сборки и т.д

2текущие изменения условий эксплуат (скорость, нагрузка, темпер и т.д)

3 качество технологич обслужив, ремонта, управление машины и т.д

В следствии выше указанных причин у однотипных машин интенсивн изменения парам технического состояния будет различна. Поэтому и момент достижен предельного состояния по наработке у них будет случайный.

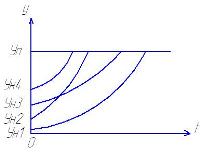
t- наработка

8 Оценка случайных величин и их практическое значение

Порядок нахождения количественных характеристик случайной величины. Последовательно начало обработки статистической информации заключ в след:

1нахождение точечных оценок случайной величины.

2нахожд вероятностных оценок случ велич и построение гистограммы распределения случ велич.

3 нахождение имперической функции вероятности отказа и вероятности безотказной работы. И построение их графиков.

4 нахождение точечных вероятностных оценок случ велич (в случае необходимости)

5предворительный выбор закона распредел случ велич.

9 Точечные оценки случайной величины

Для нахождения точечн оценок необходимо объем выборки представить в виде вариационного ряда.

Далее находят:

1.среднее значение случ велич или математич ожидание

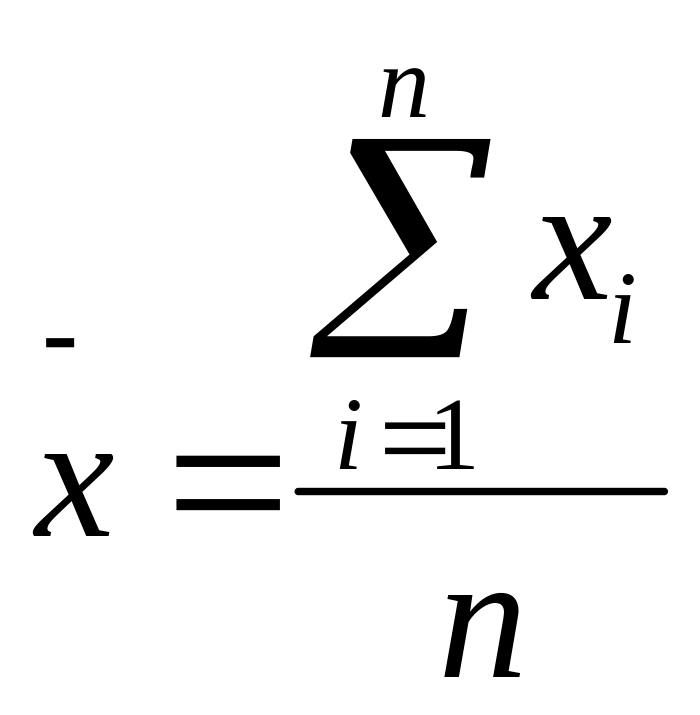
2размер случ велич:

3 среднее квадратичн отклонение случ величины

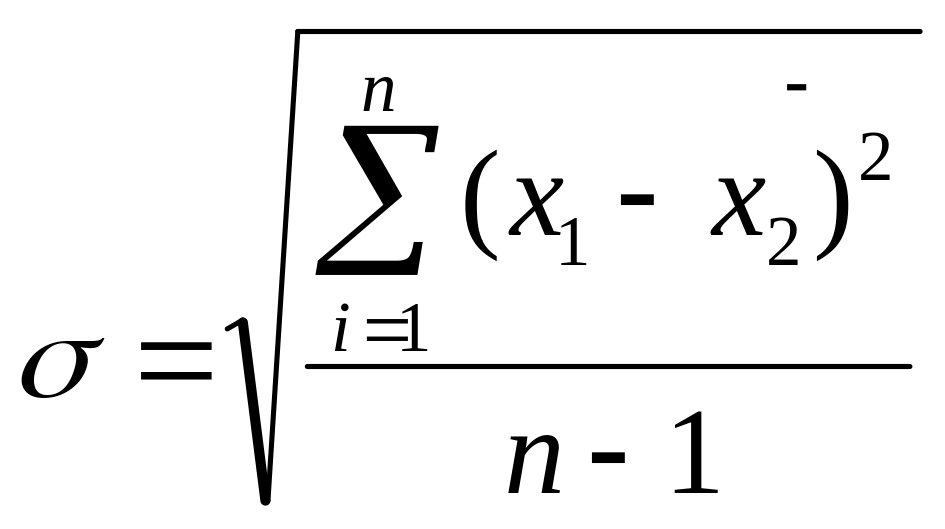
4 коэфф вариации

Точечные оценки случ велич позволяют судить о качестве изделия. Например чем ниже средний ресурс и выше вариация, тем ниже качество конструкции и кач изготов изделия.