
- •2.Глав. Вектор и глав. Момент сил.
- •3.Мом. Силы относ. Точки.Т Вариньона
- •4.Теоремы о парах сил.
- •5.Теорема о переносе сил в произвольную точку.
- •7.Расчёт ферм.
- •11.Вращательное движение вокруг неподвижной точки.Теорема Эйлера.
- •17.Силы постоян., перемен., зависящие от расстояния,зависящие от скорости,зависящие от времени.
- •19.Прицип относительности классической механики.
- •20. Теор. О движ. Ц.М. Сист.
- •22.Теор об изменении количества движения механич сист.
11.Аксиомы статики
1. Изолированная точка - это материальная точка, которая под действием сил движется равномерно прямолинейно, либо находится в состоянии относительного покоя.
2. две силы равны, если они приложены к одному телу, действуют вдоль одной прямой и направлены в противоположные стороны, такие силы называются уравновешивающими.
3. Не нарушая состояния тела к нему можно приложить или от него отбросить уравновешивающую систему сил.
Следствие: всякую силу можно переносить вдоль линии её действия, не изменяя действия силы на данное тело.
4. Равнодействующая двух сил приложенных в одной точке, приложена в той же точке и является по величине и направлению диагональю параллелограмма, построенных на данных силах.
5. Всякому действию есть равное по величине и направлению противодействие.
2.Глав. Вектор и глав. Момент сил.
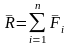 Сила
R называется главным вектором системы
сил
Сила
R называется главным вектором системы
сил
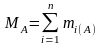 главный
момент системы сил
главный
момент системы сил
3.Мом. Силы относ. Точки.Т Вариньона
Моментом силы относительно точки (рисунок 1.1) называется векторное произведение радиус-вектора точки приложения силы на вектор силы.
Mo(F) = r ⊗ F
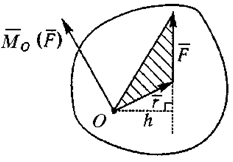
Рисунок 1.1
Вектор момента направлен перпендикулярно плоскости, в которой лежат сила и точка, в ту сторону, откуда поворот от действия силы виден происходящим против хода часовой стрелки. Вектор момента характеризует положение плоскости и направление вращательного действия силы, а также дает меру этого действия:
|Mo(F)| = F⋅r⋅sinα = F⋅h,
где h – плечо силы (кратчайшее расстояние от точки O – центра момента – до линии действия силы). Если сила проходит через точку, то ее момент относительно этой точки равен нулю.
Момент силы относительно точки не меняется от переноса силы вдоль линии ее действия.
Если силы расположены в одной плоскости, то используется понятие алгебраического момента силы.Алгебраическим моментом силы относительно точки (или центра) называется взятое со знаком плюс или минус произведение модуля силы на плечо (рисунок 1.2).
Знак плюс выбирается в том случае, если сила стремится поворачивать плоскость относительно центра момента против хода часовой стрелки.

Рисунок 1.2
Если сила F задана своими проекциями Fx, Fy, Fz на оси координат и даны координаты x, y, z точки приложения этой силы, то момент силы относительно начала координат вычисляется следующим образом:
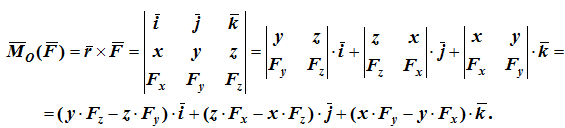
Проекции момента силы на оси координат равны
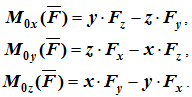
Т.Вариньона: Если система сил, приложенных к абсолютно твердому телу имеет равнодействующую, то момент равнодействующей относительно произвольного центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси).
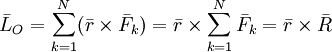 векторная
запись теоремы.
векторная
запись теоремы.
Если
имеется материальная точка
![]() ,
к которой приложена сила F
, то момент силы относительно точки O
равен векторному произведению
радиус-вектора
,
к которой приложена сила F
, то момент силы относительно точки O
равен векторному произведению
радиус-вектора
![]() , соединяющий точки O и
,
на вектор силы F
:
, соединяющий точки O и
,
на вектор силы F
:
![]()
4.Теоремы о парах сил.
Теорема 1.Две пары, лежащие в одной плоскости, можно заменить одной парой, лежащей в той же плоскости, с моментом, равным сумме моментов данных двух пар.
Теорема 2.Две пары, имеющие равные моменты, эквивалентны.
Теорема 3. Две пары, лежащие в пересекающихся плоскостях, эквивалентны одной паре, момент которой равен сумме моментов двух данных пар.
5.Теорема о переносе сил в произвольную точку.
Пусть
на тело действует система произвольно
направленных, лежащих в одной плоскости
сил ![]()
.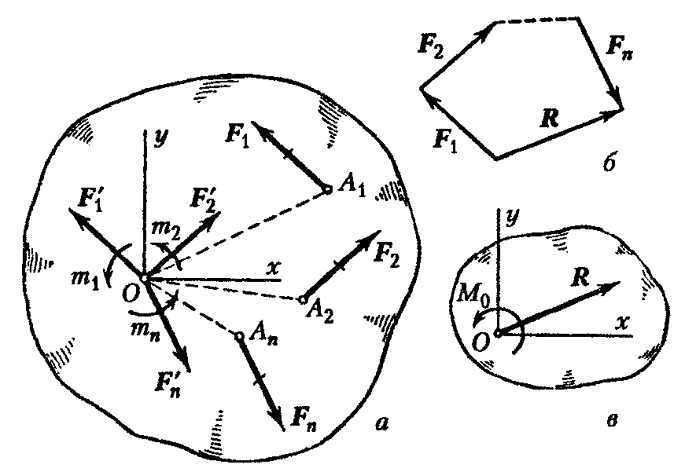
В результате получим новую систему сил:
![]()
с моментами присоединенных пар:
![]()
Систему
сил перенесенную в точку О заменим одной
силой ![]() приложенной
в той же точке О:
приложенной
в той же точке О:
![]()
Сложение пар дает одну пару с моментом:
![]()
Вектор
,
равный геометрической сумме всех сил
называют главным
вектором системы.
Величину ![]() ,
равную сумме всех моментов относительно
центра О, называют главным
моментом системы
относительно центра О.
,
равную сумме всех моментов относительно
центра О, называют главным
моментом системы
относительно центра О.
Итак: Всякая плоская система сил, действующая на твердое тело при приведении к произвольно взятому центру О заменяется одной силой , равной главному вектору системы и приложенной в Центре приведения О, и одной парой с моментом , равным главному моменту системы сил относительно центра О.
6. Аналит. усл. равновес. произвольной простр. сист. сил.
Произвольной пространственной системой сил называется система сил, линии действия которых не лежат в одной плоскости.
В аналитической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на три координатные оси и суммы моментов всех сил относительно этих осей были равны нулю
ΣFkx = 0, ΣFky = 0, ΣFkz = 0,
Mx(Fk) = 0, My(Fk) = 0, Mz(Fk) = 0.
Условия равновесия могут быть использованы для решения задач на равновесие при определении неизвестных величин (реакций связей).
Чтобы задача была статически определимой, число неизвестных должно быть не более шести.
В частности, для системы параллельных сил условиями равновесия являются следующие равенства
ΣFkx = 0, Mx(Fk) = 0, My(Fk) = 0.
