МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ,МОЛОДІ ТА СПОРТУ УКРАЇНИ

НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ “ЛЬВІВСЬКА ПОЛІТЕХНІКА”

Графічно-розрахункова робота

на тему:

«Попереднє тестування»

з курсу

“ Інтелектуальний анаіз даних. ”

Виконала

Студентка групи КН-33

Нарушинська О.О.

Прийняв

Стех Ю.В.

Львів 2013

Зміст

Вступ 3

Постановка завдання 4

Основний результат 5

Pretest-оцінка 6

WALS-оцінка 7

Теорема еквівалентності 8

Попереднє тестування і ефект «заниження» 9

Прогнозування і попереднє тестування 11

Висновки 13

Список використаних джерел 14

Вступ

Зазвичай, в економетричних дослідженнях дані не є результатом експерименту, тому ми змушені використовувати одні й ті ж дані як для вибору моделі, так і для оцінки параметрів обраної моделі. Ця обставина впливає на властивості отриманих оцінок. Зрештою все, чим займаються в економетриці , неправильно, але це не є проблемою. Проблема виникає тоді,коли ці неточності мають значний вплив.

Якщо параметри моделі оцінюються тим самим набором даних де відбувався вибір моделі, тобто після попереднього тестування, то такі оцінки називають pretest-оцінками(оцінками, отриманими після попереднього тестування).

Проблема в тому, що зазвичай, описуючи властивості отриманої оцінки, ми вважаємо, що не було попереднього відбору моделі. У результаті (помилково) вважаємо оцінку незміщеною і користуємося неправильною оцінкою її дисперсії, оскільки застосовувані нами формули для середнього та дисперсії вірні тільки умовно.

Таким чином, нашим завданням є знаходження безумовних моментів pretest-оцінки, беручи до уваги те, що процедури вибору моделі і оцінки параметрів інтегровані в одну процедуру. Ми не стверджуємо, що слід уникати попереднього тестування, хоча добре відомо, що pretest-оцінки володіють поганими статистичними властивостями, одна з яких - рівномірна неефективність. На практиці уникнути попереднього тестування майже неможливо. Наша точка зору полягає в тому, що слід обчислювати коректно зсув і дисперсію (або середньоквадратичне відхилення) оцінки, повністю беручи до уваги те, що оцінювання та відбір моделі інтегровані в одну процедуру.

Постановка завдання

В подальшому, буде розглядатися лінійна модель множинної регресії

(1)

Де у – (n×1) вектор спостережень залежної змінної, X, Z- матриці невідомих параметрів розмірами (n×k), (n×m), ɛ-( n×1)вектор помилок, β і γ – вектори невідомих(невипадкових) параметрів розмірами(k×1),( m×1). Ми припускаємо, що блочна матриця має повний ранг k+m, і помилки є незалежними нормальними однаково розподіленими випадковими величинами:

Введемо наступне позначення:

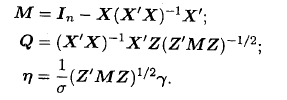(2)

Т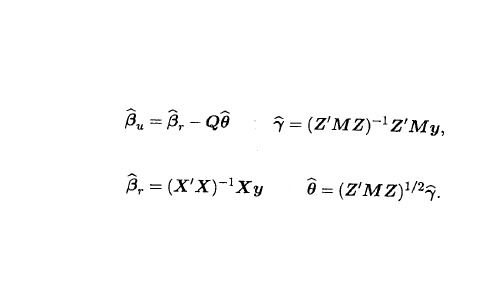 ут ɳ - нормований вектор параметрів, а матриця Q- може бути представлена як (нормована) матриця кореляцій між X та Z. Очевидно, Q=0тільки тоді , коли Z ортогональна X. МНК-оцінки параметрів β і γ можна представити у вигляді

і

де

,

Індекси u та r означають «без обмежень» і «з обмеженнями». Нехай , тоді відмітимо, що випадковий вектор є тільки тоді, коли дисперсія помилки відома, а вектор присутній завжди.