Апроксимація функції у середовищі mathcad

1. Запускаємо на виконання середовище програмування Mathcad командою Пуск | Программы | Mathcad (рис. 77).

Рис. 77

2. Користуючись відповідними панелями інструментів (вивести панелі можна командою меню View | Toolbars), заносимо початкові дані у вікно документа Mathcad: кількість точок табличної функції n, діапазон зміни індексу масивів x і y, а також елементи самих масивів.

3. Апроксимація табличної функції y многочленом першого степеня .

• Повна система рівнянь для знаходження а і b має такий вигляд:

• Внесемо у документ Mathcad формули для визначення матриці коефіцієнтів M1 і вектора V1 вільних членів системи рівнянь:

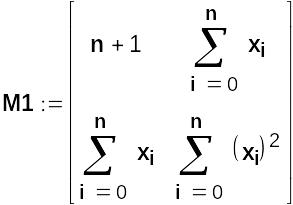
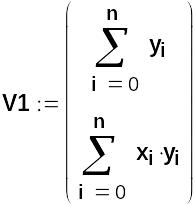
• Обчислимо значення M1 і V1:

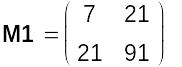
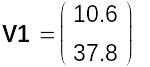
• Якщо j – це вектор, що складається із змінних а і b, то систему рівнянь можна подати у вигляді M1 j = V1. Тоді j можна знайти так:

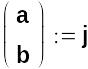
• Залишилося обчислити коефіцієнти полінома:

• Внесемо у документ формулу полінома й обчислимо його значення в таблиці (це дозволить нам пізніше відобразити криву на графіку):

4. Апроксимація функції багаточленом другого степеня .

• Система рівнянь для знаходження c, d і e має такий вигляд:

• Розширена матриця коефіцієнтів для знаходження с, d і e:

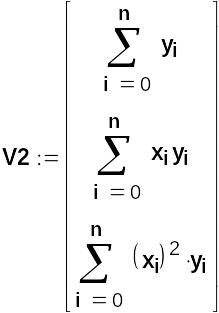
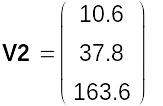
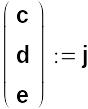
• Якщо j – це вектор, що складається з елементів c, d, e, то систему рівнянь можна подати у вигляді M2j=V2. Тоді j можна обчислити так:

• Внесемо у документ формулу полінома й обчислимо його значення у табличних вузлах.

• Тепер можна побудувати порівняльний графік функції.

5. Оцінка похибки апроксимації.

• Обчислимо нев'язку для P1(x) і вихідних даних.

• Похибка апроксимації поліномом першого степеня.

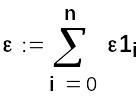
• Розрахуємо нев'язку для P2(x) і вихідних даних.

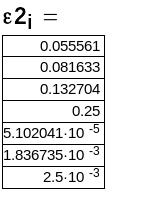
• Похибка апроксимації поліномом другого степеня.

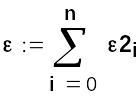
• Порівнявши одержані похибки, можна зробити висновок: апроксимація табличної функції багаточленом другого степеня P2(x) більш точна порівняно з апроксимацією багаточленом першого степеня P1(x).

6. Результати розрахунку необхідно порівняти з відповідними розрахунками в середовищах Visual C++ і Excel.

7. Документ Mathcad можна зберегти як файл з розширенням *.rtf, що дозволяє легко вставити одержані результати до пояснювальної записки, яка є документом Microsoft Word.

• Виконайте команду основного меню File | Save as. З’явиться діалогова панель «Сохранить как» (рис. 78).

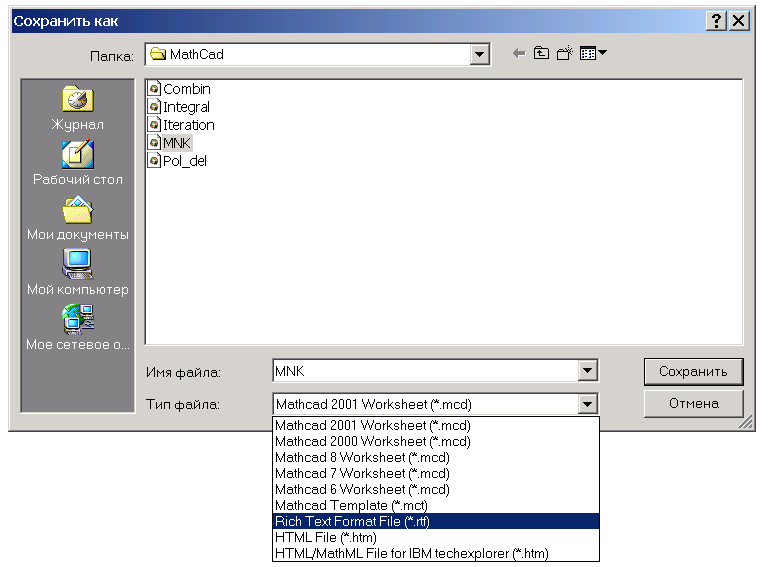
Рис. 78

• У вікні редагування «Имя файла» введіть ім’я нового файла документа (наприклад MNK).

• У списку «Тип файла» виберіть розширення Rich Text Format File (*.rtf).

• Завершіть роботу з панеллю «Сохранить как», натиснувши на кнопку «Сохранить».

ДОДАТОК 1

Метод найменших квадратів

Нехай у результаті експерименту одержано таблицю значень функції:

x	x0	x1	x2	...	xn
y	y0	y1	y2	...	yn

Необхідно апроксимувати цю табличну функцію багаточленом степеня m (m < n):

. (Д.1.1)

Згідно з методом найменших квадратів (МНК) шукаємо значення параметрів , при яких сума квадратів різниць

(Д.1.2)

набуває мінімального значення:

. (Д.1.3)

З урахуванням необхідних умов існування екстремуму функції декількох змінних одержуємо систему рівнянь для визначення невідомих :

(Д.1.4)

Доведено, що система рівнянь має єдиний розв’язок, при якому набуває мінімального значення.

Розглянемо випадок m = 2, тобто табличну функцію апроксимуємо багаточленом другого степеня .

Система рівнянь для визначення параметрів має такий вигляд:

(Д.1.5)

Якщо розв’язати систему рівнянь, можна записати багаточлен .