Тема 5.Средние величины и показатели вариации.
1. Понятие средней величины (СВ). Способы расчета средней.
2. Структурные средние.
3. Показатели вариации.
1. Понятие средней величины (СВ). Способы расчета средней.
Каждая однородная статистическая совокупность состоит из массы отдельных единиц, кот. обладают индивидуальными особенностями и поэтому отличаются друг от друга по размеру кол-ного признака.
Для получения обобщающей хар-ки большого кол-тва индивид. значений варьирующего признака рассчитываются средние величины.
Следует отметить, что к средней величине обращаются не только тогда, когда речь идёт о вариации признака, но и когда необходимо дать обобщающую инф-цию по всей совокупности.
Под средней величиной понимают обобщающий показатель, хар-щий типичный уровень или размер варьирующего признака в расчете на единицу однородной совокупности в конкретных условиях места и времени.
Таким образом средняя величина – это величина, кот. одним значением хар-ет нечто общее для совокупности в целом.
Средняя величина в статистике:
1) хар-ет типичный уровень варьирующего признака;
2) отражает то общее, что хар-но для всех единиц совокупности;
3) взаимопогашает различия, кот. наблюдаются у отдельных единиц совокупности.
Средние величины могут быть исчислены по непосредственному перечню значений варьирующего признака у каждой единицы совокупности.
Т.е. средняя величина может быть рассчитана по первичным несгруппированным данным и по сгруппированным данным. Такие средние назыв. простыми и взвешенными.
Если средние вычисляются по варьирующему ряду сгруппированной инф-ции с учетом статистического веса каждого варианта, то их назыв. взвешенными средними.
Способы расчета средней зависят:
1) от того какой инф-цией мы обладаем для расчета средней;
2) от хар-ра осреднённой величины.
Исходной базой расчета и критерием правильности выбора формы средней величины явл. исходное соотношение средней или смысловая формула.
Смысловая формула – это словесное описание методологии расчета средней величины.
Общий вид смысловой формулы:
Для каждого среднего показателя используемого в соц.-экон. анализе можно составить только одну смысловую формулу для расчета среднего показателя.
Пример.
Составим смысловую формулу для расчета средней ЗП.
Средняя цена ед. продукции:
Средний стаж 1-го работника:
Средний процент выполнения плана по выпуску про-ции:
Выбор формы и вида средней величины происходит след. образом:
1) если известен знаменатель смысловой формулы и неизвестен числитель, то используют среднюю арифметическую;
2) если известен числитель смысловой формулы и неизвестен знаменатель, то выбираем форму средней гармонической;
3) если исходная инф-ция несгруппирована, то используют простую среднюю;
4) если исходная инф-ция сгруппирована, то используют среднюю взвешенную.
В статистике применяются 2 наиболее распространённых вида средней величины: средняя арифметическая и средняя гармоническая. При этом каждый из этих видом может иметь 2 формы: простую или взвешенную.
Средняя арифметическая простая – это отношение суммы значений признака в отдельных единицах совокупности к числу единиц совокупности.
x – значение признака в каждой единицы совокупности
n – кол-тво единиц совокупности.
Средняя арифметическая взвешенная – это отношение общего размера значений признака во всех единицах сгруппированной совокупности к численности единиц во всех группах.
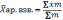
m – веса, т.е. число ед. совокупности в каждой отдельной группе или может быть удельный вес каждой отдельной группы.
Средняя гармоническая простая – это обратное значение средней из обратных значений варьирующего признака, т.е. вариантов.
Средняя гармоническая взвешенная – это обратное значение средней из обратных значений варьирующего признака во всех единицах сгруппированной совокупности.
Для наглядности нарисуем схему форм и видов средних величин:
Средние величины: |
|||
Формы: |
Виды: |
||
простая |
взвешенная |
суммарные: |
структурные |
|
|
- параболические; - логарифмические; - степенные (арифметическую, гармоническую, гармоническую |
- мода; - медиана; - децили; - квартили |
Пример.
По пр-ю, занимающемуся торговлей ценных бумаг, имеются данные о приобретении акций в 2-х акционерных обществах.
АО |
Август |
Сентябрь |
|||
Кол-тво приобр. акций, шт (m) |
Цена 1 акции, грн (x) |
Стоим-ть приобр. акций, грн (m) |
Цена 1 акции, грн (x) |
||
№1 |
600 |
11 |
6000 |
12 |
|
№2 |
900 |
14 |
6400 |
16 |
|
Итого |
1500 |
х |
12400 |
х |
|
Опр-ть среднюю цену одной приобретённой акции по 2-м акционерным обществам в августе и сентябре.
Как изменилась средняя цена акции в абсолютном и относительном выражении.
Т.к. инф-ция сгруппирована и в смысловой формуле известен знаменатель и неизвестен числитель будем использовать среднюю арифметическую взвешенную.
В августе по 2-м акционерным обществам акции скупали в среднем по цене 12,80 (грн) за единицу.
Т.к. в сентябре месяце в смысловой формуле известен числитель и неизвестен знаменатель, инф-ция сгруппирована, веса неравны, то будем использовать среднюю гармоническую взвешенную.
В сентябре по 2-м АО в среднем скупали по 13,78 грн за единицу.
Абсолютное значение изменения ед. акции:
Относительное значения изменения ед. акции:
14.09.
В сентябре месяце по сравнению с августом средняя цена одной акции выросла на 0,98 грн или в 1,077 раза, т.е. на 7,7%