
- •4,Ошибка воспроизведения.
- •5. Основные принципы управления. Разомкнутые системы. Управление с внутренней моделью.
- •6. Селективная инвариантность до при гармоническом задающем воздействии.
- •Вопрос 7. Описание звеньев сау. Уравнение звена в изображениях и передаточная функция.
- •Операторная (символическая) форма записи уравнения элемента
- •8 Чувствительность систем управления к изменению параметров
- •10. Понятие об инвариантных системах
- •12.Понятие о качестве сау. Точность работы сау в установившемся режиме.
- •1. Понятие о качестве системы
- •2. Точность работы сау в установившемся режиме.
- •13 Передаточные функции сау с прямой и обратой связью
- •14. Логарифмические частотные характеристики основных сомножителей передаточной функции
- •15. Реакция линейной замкнутой системы на внешние воздействия. Ду замкнутой системы. Пример
- •16. Вычисление коэффициентов ошибок с помощью передаточной функции по ошибке. Пример.
- •Вопрос17. Стандартная форма представления передаточной функции разомкнутой системы.
- •20. Функция чувствительности и дополнительная функция чувствительности. Интуитивные требования к выбору управляющего устройства.
- •21. Корневые методы оценки качества переходного процесса. Оценка быстродействия.
- •22. Математическая модель двигателя постоянного тока
- •23 Понятие об устойчивости сау
- •24. Селективная абсолютная инвариантность к задающему воздействию в системах с единичной обратной связью. Принцип внутренней модели.
- •25. Алгебраический критерий устойчивости Гурвица.
- •26. Правила преобразования структурных схем.
- •27. Относительная устойчивость.
- •30( Как62). Фомирование частотных характеристик замкнутой системы. Ограничения на дополн. Ф-ю чувств. Смешанн чувствит.
- •32. Коррекция системы с опережением по фазе(реальный пд-регулятор)
- •34. Коррекция с помощью ку с отставанием по фазе
- •35. Уравнение звена в символической форме.
- •36. Понятие о корневом годографе.
- •Вопрос 37. Описание элементов сау. Линеаризация.
- •38 Понятие о коэффициентах ошибок
- •Вычисление коэффициентов ошибок с помощью пф по ошибке
- •39. Передаточные функции системы с единичной обратной связью.
- •40. Критерий Найквиста для случая устойчивой разомкнутой системы. Критический коэффициент усиления.
- •41. Критерий Найквиста для случая неустойчивой разомкнутой системы.
- •42. Линеаризация математической модели бака с жидкостью.
- •43 Понятие о коэффициентах ошибок
- •Коэффициенты ошибок статических и астатических систем.
- •44.(Вкл в себя72) Количественная оценка неопределенностей модели объекта
- •45. Типовые динамические звенья и их характеристики. Интегрирующее звено. Дифференцирующие и форсирующие звенья.
- •46. Критерий Найквиста для случая нейтрально-устойчивой разомкнутой системы.
- •Вопрос 47. Афх разомкнутой системы и ее предельные значения.
- •1) Замкнутая система неустойчива
- •50. Обеспечение астатизма по возмущающему воздействию.
- •2) Уравнение звена в изображениях. Передаточная функция звена (пф)
- •53 Минимально-фазовые звенья
- •54. Введение связей по возмущению
- •55. Построение лчх разомкнутой системы. Правила построения лачх. Пример.
- •56. Частотные методы оценки качества переходного процесса.
- •Вопрос 57. Ошибка по возмущению.
- •58 Робастное качество.
- •59.Задача слежения и регулирования. Возмущения и ограничения.
- •60. Критерий Михайлова.
- •61. Показатели качества работы сау в переходном процессе при ступенчатом воздействии
- •62. Формирование частотных характеристик замкнутой системы
- •64, Параметрический синтез сау по методу лчх
- •65. Понятие о синтезе системы. Требования к проектируемой системе.
- •66. Методы робастного управления
- •67. Устойчивость по входу.
- •71.Внутренняя устойчивость замкнутой системы.
- •72. (Из44) Аддитивная и мультикативная неопределенности.Представление неопределенности в частотной (комплексной) области.
32. Коррекция системы с опережением по фазе(реальный пд-регулятор)
а) КУ
с опережением по фазе.
Его ПФ:
![]() .
.
Параметры КУ:q1=T, q2=α, q3=k2, α< 1,где 1/α – коэффициент опережения по фазе.
Построим ЛЧХ КУ (см. рис. ниже). Положим k2=1. Найдем сопрягающие частоты:
1=1/T, 2=1/αT.Т. к.α< 1, то 2> 1.
Т ак
как
ак
как
![]() ,
то
,
то
![]() .
.
Выражение для ЛФЧХ: φ2( )=arctg T- arctgα T.
Известно, что
![]() .
.
Полагая x=
T,
y=α
T,
получаем![]() .
.
Дифференцируя
φ2(
)по
,
находим![]() (*)
(*)
и максимум
![]() .
.
График зависимости
![]() изображен на рисунке:
изображен на рисунке:
М ожно
показать, что
ожно
показать, что![]() .Отсюда
получаем аналитическое выражение
.Отсюда
получаем аналитическое выражение![]() .
(**)
.
(**)
Если α=0,
то
![]() - ПД-регулятор.
- ПД-регулятор.
Необходимо выбрать
α
и Т так,
чтобы система удовлетворяла заданным
требованиям. При этом обычно пытаются
расположить частоту
![]() вблизи желаемой частоты среза таким
образом, чтобы желаемая частота среза
оказалась примерно посредине между
частотами
1
и
2.
Т.к. с уменьшением α
увеличивается усиление на высоких
частотах, что сопряжено с ослаблением
помехоустойчивости (зашумленности
управляющего воздействия), то приходится
искать компромиссное решение между
желанием добиться дополнительно большого
значения фазового угла и неблагоприятной
тенденцией получить большое усиление
на высоких частотах (большое усиление
шума измерения). Так обычно пытаются
взять
вблизи желаемой частоты среза таким
образом, чтобы желаемая частота среза
оказалась примерно посредине между
частотами
1
и
2.
Т.к. с уменьшением α
увеличивается усиление на высоких
частотах, что сопряжено с ослаблением
помехоустойчивости (зашумленности
управляющего воздействия), то приходится
искать компромиссное решение между
желанием добиться дополнительно большого
значения фазового угла и неблагоприятной
тенденцией получить большое усиление
на высоких частотах (большое усиление
шума измерения). Так обычно пытаются
взять
![]() ,
что означает
,
что означает
![]() .
Если требуется больший положительный
сдвиг по фазе, то используют несколько
последовательно включенных КУ с
опережением по фазе.
.
Если требуется больший положительный
сдвиг по фазе, то используют несколько
последовательно включенных КУ с
опережением по фазе.
б) Выбор параметров α и Т корректирующего устройства с опережением по фазе.
Пусть заданы требуемые значения коэффициента усиления k* и запаса устойчивости по фазе γ*.
Изменим коэффициент k1 нескорректированной системы так, чтобы коэффициент усиления скорректированной системы был равен требуемому значению k*, т.е., чтобы выполнялось условие: k=k*.
1. Построим ЛЧХ нескорректированной системы L1( ) и φ1 ( ) и определим запас устойчивости по фазе
γ 1=1800+φ1(
c),
где
c
– частота среза нескорректированной
системы. Нескорректированная система
при высоких значениях k1
оказывается неустойчивой или весьма
колебательной, т.е. γ1
< γ*
1=1800+φ1(
c),
где
c
– частота среза нескорректированной
системы. Нескорректированная система
при высоких значениях k1
оказывается неустойчивой или весьма
колебательной, т.е. γ1
< γ*
2. Определим
разность между γ1
и γ*
![]() .
.
3. Выбираем параметр
α
из условия![]() ,
используя для этой цели формулу
(**) для
,
используя для этой цели формулу
(**) для![]() или графическую зависимость
или графическую зависимость
![]() .
.
4. Определяем
частоту среза скорректированной системы
c*,
исходя из
![]() .
.
5. Полагая
*=
c*,
находим параметр
![]() и сопрягающие частоты
1=1/T,
2=1/αT.
и сопрягающие частоты
1=1/T,
2=1/αT.
6. По формулам
![]() строим ЛЧХ скорректированной системы
и определяем, удовлетворяет ли система
требованиям с точки зрения запаса
устойчивости по фазе.
строим ЛЧХ скорректированной системы
и определяем, удовлетворяет ли система
требованиям с точки зрения запаса
устойчивости по фазе.
Действительно, если вычисления выполнены точно, то
![]() ,
и L(
)
должна пересекать ось частот при
=
c*,
так что
c*=
*.
,
и L(
)
должна пересекать ось частот при
=
c*,
так что
c*=
*.
М аксимальный
сдвиг по фазе
аксимальный
сдвиг по фазе
![]() должен быть при
c*.
Если
должен быть при
c*.
Если
![]() ,
то процесс синтеза заканчивается, если
нет, то необходимо варьировать параметры.
,
то процесс синтеза заканчивается, если
нет, то необходимо варьировать параметры.
Достоинства:
1. КУ с опережением по фазе не затрагивает низкочастотного участка ЛАЧХ, т.е. не влияет на заданную точность работы системы в установившемся режиме.
2. Добились желаемого запаса устойчивости по фазе γ*, повышает запасы устойчивости.
3. c*> c , следовательно, увеличивается полоса пропускания (ПП) и увеличивается быстродействие.
Недостатки:
1. Увеличение полосы пропускания влечет за собой снижение помехоустойчивости.
2. Увеличение быстродействия связано с увеличением управляющего воздействия u(t), что может повлечь за собой выход системы из строя или заставить работать систему в нелинейном режиме. Поскольку при синтезе все элементы предполагались линейными, то влияние нелинейностей в рамках линейной теории оценить невозможно.
Процесс проектирования слегка упрощается, если мы ставим задачу спроектировать КУ с опережением по фазе при заданной частоте среза c* и заданном запасе устойчивости γ*:
Определяем требуемое значение
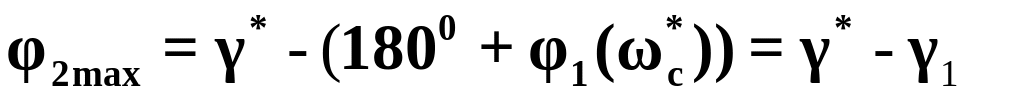 ;
;Находим ;
Находим параметр и частоты 1=1/T, 2=1/αT;
 5. Выбираем
коэффициент усиления k2
так,
чтобы ЛАЧХ скорректированной системы
пересекла ось частот при частоте
c*
.
5. Выбираем
коэффициент усиления k2
так,
чтобы ЛАЧХ скорректированной системы
пересекла ось частот при частоте
c*
.
Техническая реализация КУ с опережением по фазе
![]() ,где
,где![]() .
.
Коэффициент усиления нескорректированной системы надо увеличить в 1/α, чтобы включение цепи не повлекло за собой уменьшение коэффициента усиления системы.
Вопрос № 33(+55) Логарифмические частотные характеристики (диаграммы Боде)
Анализ и синтез САУ удобно выполнять, используя логарифмические частотные характеристики (ЛЧХ), что объясняется простотой их построения.
ЛЧХ называют
построенные в логарифмическом масштабе
частотные характеристики R(
)
и
![]() .
Для фиксированной частоты значение
R(
)
– отношение амплитуд гармонических
сигналов на входе и на выходе звена.
Если на входе и выходе сигналы одной
физической природы, то
.
Для фиксированной частоты значение
R(
)
– отношение амплитуд гармонических
сигналов на входе и на выходе звена.
Если на входе и выходе сигналы одной
физической природы, то
![]() есть натуральное число, показывающее
во сколько раз больше амплитуда выходного
сигнала Авых
, чем амплитуда входного сигнала Авх.
Это число может с изменением частоты
изменяться в очень широких пределах,
что создает трудности при построении
ЛЧХ. Поэтому в качестве единицы измерения
используют такую единицу измерения как
децибел (дБ).
Число R,
выраженное в децибелах, определяется
так:
есть натуральное число, показывающее
во сколько раз больше амплитуда выходного
сигнала Авых
, чем амплитуда входного сигнала Авх.
Это число может с изменением частоты
изменяться в очень широких пределах,
что создает трудности при построении
ЛЧХ. Поэтому в качестве единицы измерения
используют такую единицу измерения как
децибел (дБ).
Число R,
выраженное в децибелах, определяется
так:
L=20lgR [дБ] .
Значения ФЧХ при построении ЛЧХ обычно измеряют в градусах или радианах.
Дадим определение ЛЧХ с учетом замечаний относительно единиц измерения.
Определение.
Логарифмической амплитудно-частотной
характеристикой (ЛАЧХ) называют график
зависимости L(![]() )=20lgR(
),
построенный в логарифмическом масштабе
частот lg
.
)=20lgR(
),
построенный в логарифмическом масштабе
частот lg
.
Определение. Логарифмической фазо-частотной характеристикой называется график зависимости , построенный в логарифмическом масштабе частот lg .
Построение логарифмической оси частот
Возьмем частоты, кратные десяти:
=![]()
Найдем lg =i и на оси абсцисс отложим значения lg , а около засечек запишем значения самой частоты (см. рисунок) Если теперь уберем с оси значения lg , то получим логарифмическую ось частот.

Логарифмическая ось равномерна относительно частот, кратных 10.
Так же можно получить точки на оси частот для частот, некратных 10, например: =2, lg2=0,3.
Говорят, что если частота изменилась в 10 раз, то она изменилась на декаду, т.е. логарифмическая ось фактически разбита на декады.
Размерность
угловой частоты: [
]=[рад/с]
записывают как
[![]() ]
]
Частотные характеристики звеньев должны начинаться с какой-то частоты. Логарифмическая ось частот начинается в бесконечности, т.к. логарифм нуля не существует.
Поэтому обычно ось ординат проводится на такой частоте, чтобы все характерные особенности ЛЧХ оказались справа от этой оси.
