27.Проводники в электростатике. Емкость проводника. Емкость плоского конденсатора.

В конденсированных средах все электрические заряды делятся насвязанные заряды, которые входят в состав отдельных атомов и могут перемещаться только в пределах этих атомов, и на свободные заряды, которые принадлежат сразу всем атомам среды и могут перемещаться по всей среде. Концентрация и подвижность свободных зарядов определяют способность среды проводить электрический ток. Для однородной и изотропной средысопротивление   постоянному току описывается формулой

,                                                                                     (4.1)

где   - удельное сопротивление среды,   - длина среды в направлении протекания тока и   - площадь поперечного сечения среды, которая считается постоянной.

По величине удельного сопротивления все конденсированные среды условно делятся на три группы:

1. проводники, где  ;

2. полупроводники, где   при   (удельное сопротивление полупроводников сильно зависит от температуры  );

3. диэлектрики, где  .

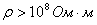Хорошими проводниками являются металлы, в которых свободными носителями заряда служат электроны проводимости с концентрацией ~ . Электроны проводимости есть коллективизированные (обобществлённые) валентные электроны атомов металла. В классической физике для описания электронов проводимости используется модель идеального газа.

Для идеального проводника  . Идеальными проводниками можно считать сверхпроводники, у которых при температуре ниже некоторой критической температуры сопротивление постоянному току обращается в нуль. Допустим, что такой идеальный проводник помещён в постоянное электрическое поле  , созданное некоторой системой неподвижных зарядов. Под действием электрического поля в проводнике начнётся пространственное перераспределение свободных зарядов, которое прекратится только тогда, когда полное электрическое поле во всех точках внутри проводника

.                                                               (4.2)

Полное поле   есть сумма внешнего поля   и поля  , созданного перераспределёнными зарядами проводника, которые называются индуцированными. Условие (4.2) может быть выполнено для всех точек внутри проводника только в том случае, если индуцированные заряды распределены в тонком поверхностном  слое проводника толщиной порядка одного атомного слоя.

За пределами проводника полное электрическое поле  . Рассмотрим поверхность  , которая разделяет проводник и вакуум (рис. 4.1). Выберем на поверхности раздела   произвольную точку   и проведём в этой точке перпендикуляр к данному элементу поверхности. На построенном перпендикуляре возьмём точки 1 и 2, находящиеся на бесконечно малом расстоянии от точки  , причём точка 1 находится внутри проводника, а точка 2 – в вакууме.

Используя теорему Гаусса и теорему о циркуляции вектора напряжённости электрического поля, можно показать, что поля   и   в точках 1 и 2 соответственно связаны между собой следующими граничными условиями:

      .                                                     (4.3)

Рис. 4.1

Здесь   и   - проекции вектора напряжённости электрического поля  в точке  ,  , 2 на направления соответственно единичного вектора нормали   и единичного вектора касательной   к поверхности в точке  ,   - поверхностная плотность зарядов точке и  - электрическая постоянная.

Из граничных условий (4.3) с учётом (4.2) следует, что

          .                                   (4.4)

Таким образом, вектор напряжённости полного электрического поля вблизи поверхности проводника всегда перпендикулярен этой поверхности, а его величина формально определяется поверхностной плотностью индуцированных зарядов.

Если проводнику передать некоторый заряд, то он распределится по внешней поверхности этого проводника таким образом, чтобы во всех точках проводника электрическое поле равнялось нулю. Таким образом, как во внешнем электростатическом поле, так при зарядке проводника потенциал полного электрического поля во всех точках проводника является постоянным

.                                                                                  (4.5)

В общем случае распределение зарядов по поверхности проводника не является равномерным. Наибольшая поверхностная плотность зарядов наблюдается в тех точках, где главные радиусы кривизны поверхности наименьшие (края, выступы, заострения поверхности).

Отметим, что характерное время установления локального равновесного распределения зарядов в металле

,

где   - масса электрона,   - заряд электрона,   - концентрация свободных электронов в металле и   - электропроводность металла. Оценка показывает, что для меди характерное время установления равновесного распределения зарядов всего ~ .

Проводящие поверхности и достаточно густые металлические сетки используются для защиты от действия внешнего электрического поля. Если электрические заряды находятся в области, ограниченной заземлённым металлическим экраном (экраном, соединённым с проводящей Землёй), то полное электрическое поле во всей внешней области, созданное зарядами внутри экрана и зарядами, индуцированными на экране, равно нулю. При этом заряд, индуцированный на экране, равен по величине полному заряду внутри экрана, но имеет противоположный знак. Таким образом, суммарный заряд, включая первичные заряды и индуцированные заряды на экране, равен нулю.