[Править]Закон Пуазёйля (Хагена — Пуазёйля)

Основная статья: Закон Пуазёйля

Уравнение или закон Пуазёйля (закон Хагена — Пуазёйля или закон Хагена — Пуазёйля) — закон, определяющий расход жидкости при установившемся течении вязкой несжимаемой жидкости в тонкой цилиндрической трубе круглого сечения.

Сформулирован впервые Готтхильфом Хагеном (нем. Gotthilf Hagen, иногда Гаген) в 1839 году и вскоре повторно выведен Ж. Л. Пуазёйлем (фр. J. L. Poiseuille) в 1840 году. Согласно закону, секундный объёмный расход жидкости пропорционален перепаду давления на единицу длины трубки (градиенту давления в трубе) и четвёртой степени радиуса (диаметра) трубы:

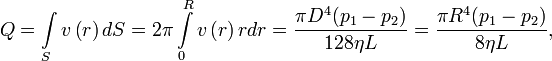
где

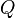•  — расход жидкости в трубопроводе;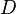

•  — диаметр трубопровода;

Закон Пуазёйля работает только при ламинарном течении и при условии, что длина трубки превышает так называемую длину начального участка, необходимую для развития ламинарного течения в трубке.

[Править]Свойства

• Течение Пуазёйля характеризуется параболическим распределением скорости по радиусу трубки.

• В каждом поперечном сечении трубки средняя скорость вдвое меньше максимальной скорости в этом сечении.

[Править]Применимость на практике

• Для расчета бытовых водопроводов расчет по формуле Пуазёйля дает ошибку в разы, потому что течение в них обычно не ламинарное, а турбулентное и не учитывает шершавость стенок. Лучше использовать специальные калькуляторы.

10.Теория относительности. Мировые линии. Интервал. Преобразования Лоренца. Сокращение длины. Замедление времени. Энергия и импульс.

Относительности теория

Относительности теория, физическая теория, рассматривающая пространственно-временные свойства физических процессов. Закономерности, устанавливаемые О. т., являются общими для всех физических процессов, поэтому часто о них говорят просто как о свойствах пространства-времени. Как было установлено А. Эйнштейном, эти свойства зависят от гравитационных полей (полей тяготения), действующих в данной области пространства-времени. Свойства пространства-времени при наличии полей тяготения исследуются в общей теории относительности (ОТО), называются также теорией тяготения. В частной теории относительности рассматриваются свойства пространства-времени в приближении, в котором эффектами тяготения можно пренебречь. Логически частная О. т. есть частный случай ОТО, откуда и происходит её название. Исторически развитие теории происходило в обратном порядке; частная О. т. была сформулирована Эйнштейном в 1905, окончательная формулировка ОТО была дана им же в 1916. Ниже излагается частная О. т., называется в литературе также теорией относительности Эйнштейна, просто О. т., или специальной теорией относительности (история её возникновения изложена в последнем разделе).

Основные черты теории относительности

Явления, описываемые О. т. и называемые релятивистскими (от лат. relatio — отношение), проявляются при скоростях движения тел, близких к скорости света в вакууме с = (2,997924562 ± 0,000000011) ´ 10¹⁰см/сек. При таких скоростях (называемых релятивистскими) зависимость энергииЕ тела от его скорости v описывается уже не формулой классической механики Е_кин = mu²/2, а релятивистской формулой

  (1)

Масса т, входящая в эту формулу, в О. т. называется также массой покоя. Из (1) видно, что энергия тела стремится к бесконечности при скорости u, стремящейся к с, поэтому если масса покоя не равна нулю, то скорость тела всегда меньше с, хотя при Е >> mc ²она может стать сколь угодно близкой к с. Это непосредственно наблюдается на ускорителях протонов и электронов, в которых частицам сообщаются энергии, много большие mc ², и поэтому они движутся со скоростью, практически равной с. Со скоростью света всегда движутся частицы, масса покоя которых равна нулю (фотоны — кванты света, нейтрино). Скорость с является предельной скоростью передачи любых взаимодействий и сигналов из одной точки пространства в другую.

Существование предельной скорости вызывает необходимость глубокого изменения обычных пространственно-временных представлений, основанных на повседневном опыте. Рассмотрим следующий мысленный опыт. Пусть в вагоне, движущемся со скоростью u относительно полотна железной дороги, посылается световой сигнал в направлении движения. Скорость сигнала для наблюдателя в вагоне равна с. Если бы длины и времена, измеряемые любым наблюдателем, были одинаковы, то выполнялся бы закон сложения скоростей классической механики и для наблюдателя, стоящего у полотна, скорость сигнала была бы равна с + u, т. е. была бы больше предельной. Противоречие устраняется тем, что в действительности с точки зрения наблюдателя, относительно которого физическая система движется со скоростью u, все процессы в этой системе замедляются в    раз (это явление называется замедлением времени), продольные (вдоль движения) размеры тел во столько же раз сокращаются и события, одновременные для одного наблюдателя, оказываются неодновременными для другого, движущегося относительно него (т. н. относительность одновременности). Учёт этих эффектов приводит к закону сложения скоростей, при котором предельная скорость оказывается одинаковой для всех наблюдателей.

Характерное для О. т. явление замедления времени может принимать огромные масштабы. В опытах на ускорителях и в космических лучах образуются распадающиеся (нестабильные) частицы, движущиеся со скоростью, близкой к скорости света. В результате замедления времени (с точки зрения земного наблюдателя) времена их распада и, следовательно, проходимые ими (от рождения до распада) расстояния увеличиваются в тысячи и десятки тысяч раз по сравнению с теми, которые частицы пролетали бы, если бы эффект замедления времени отсутствовал.

Из релятивистской формулы для энергии следует, что при малых скоростях (u << с) энергия тела равна

Второй член справа есть обычная кинетическая энергия, первый же член показывает, что покоящееся тело обладает запасом энергии E_o = mc ², называющейся энергией покоя (т. н. принцип эквивалентности энергии и массы, или принцип эквивалентности Эйнштейна).

В ядерных реакциях и процессах превращений элементарных частиц значительная часть энергии покоя может переходить в кинетическую энергию частиц. Так, источником энергии, излучаемойСолнцем, является превращение четырёх протонов в ядро гелия; масса ядра гелия меньше массы четырёх протонов на 4,8×10^–26г, поэтому при каждом таком превращении выделяется 4,3×1^–5эргкинетической энергии, уносимой излучением. За счёт излучения Солнце теряет в 1 сек 4×10⁷т своей массы.

О. т. подтверждена обширной совокупностью фактов и лежит в основе всех современных теорий, рассматривающих явления при релятивистских скоростях. Уже последовательная теория электромагнитных, в частности оптических, явлений, описываемых классической электродинамикой (см. Максвелла уравнения), возможна только на основе О. т. Теория относительности лежит также в основе квантовой электродинамики, теорий сильного и слабого взаимодействий элементарных частиц. Законы движения тел при релятивистских скоростях рассматриваются в релятивистской механике, которая при скоростях u << с переходит в классическую механику Ньютона. Квантовые законы движения релятивистских микрочастиц рассматриваются в релятивистской квантовой механике и квантовой теории поля.

Мирова́я ли́ния в теории относительности — кривая в пространстве-времени, описывающая движение тела (рассматриваемого какматериальная точка), геометрическое место всех событий существования тела. Иногда мировой линией называют вообще любую непрерывную линию в пространстве-времени.

Нормированный касательный вектор к мировой линии тела называется его 4-скоростью и должен лежать внутри светового конуса будущего. Мировая линия массивного тела является времениподобной кривой, то есть скалярный квадрат касательного вектора в любой её точке строго положителен в сигнатуре (+,−,−,−) (или строго отрицателен в сигнатуре (−,+,+,+)). В этом случае натуральный параметр(канонический параметр) мировой линии называется собственным временем тела и совпадает со временем, измеренным идеальными часами, следующими вместе с телом.

Вектор кривизны мировой линии тела называется его 4-ускорением.

Интервал в теории относительности — аналог расстояния между двумя событиями в пространстве-времени, являющийся обобщением евклидового расстояния между двумя точками. Интервал лоренц-инвариантен, то есть не меняется при переходе от одной инерциальной системы отсчёта к другой, и, даже более, является инвариантом(скаляром) в специальной и общей теории относительности.

Это свойство интервала делает его фундаментальным понятием, на основе которого может, в соответствии с принципом относительности, быть осуществлена ковариантная формулировка физических законов. В частности, преобразования Лоренца (преобразования координат, включая время, оставляющие неизменной запись всех фундаментальных уравнений физики при замене системы отсчёта) могут быть формально найдены как группа преобразований, сохраняющих интервал инвариантным.

Инвариантность интервала послужила основой для введения пространства Минковского, в котором смене инерциальных систем отсчёта соответствуют «вращения» этого пространства, что явилось первой явной формулировкой концепции пространства-времени.