§ 9. Видимі рухи планет. Закони Кеплера

1. Нижні й верхні планети. За особливостями свого видимого руху на небесній сфері планети поділяються на дві групи: нижні (Меркурій, Венера) і верхні (Марс, Юпітер, Сатурн, Уран, Нептун і Плутон). Рух верхніх і нижніх планет по небесній сфері відбувається по-різному.

Меркурій і Венера розташовуються на небі в тих же сузір'ях, що й Сонце, або в сусідні. При цьому вони можуть перебувати як на захід, так і на схід від нього, але не далі 28^о (Меркурій) і 48^о (Венера).

Найбільше кутове відхилення планети від Сонця на схід називається найбільшою східною елонгацією (від панцира. - «віддаляюся»), на захід - найбільшою західною елонгацією.

У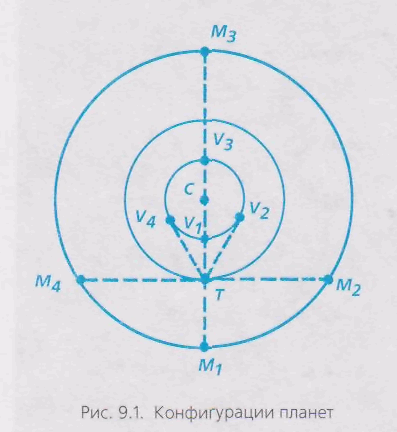 випадку східної елонгації планету видно на заході в променях вечірньої заграви незабаром після заходу Сонця (мал. 9.1, положення У_А), через якийсь час вона також заходить. Далі, переміщаючись у зворотному напрямку (зі сходу на захід, проти видимого руху Сонця), спочатку повільно, а потім усе швидше планета починає наближатися до Сонця, ховається в його променях і стає невидимою. У цей час планета проходить між Землею й Сонцем і відбувається її нижня сполука із Сонцем (мал. 9.1, положення V₁).

Незабаром після нижньої сполуки планета стає видимою на сході, у променях ранкової зорі, незадовго до сходу Сонця. Продовжуючи переміщатися у зворотному напрямку, планета досягає найбільший західної елонгації (мал. 9.1, положення М₁), зупиняється на якийсь час і знову починає свій рух, але вже прямо, із заходу на схід, у напрямку до Сонця.

Повернувшись до Сонця, планета на певний час зникає в його променях і знову стає невидимою. У цей час вона проходить за Сонцем, і відбувається її верхня сполука (мал. 9.1, положення М₃), після чого через деякий час вона вже видна на заході в променях вечірньої заграви. Далі цикл повторюється.

Таким чином, нижні планети «коливаються» щодо Сонця.

Інакше відбувається видимий рух верхніх планет. Коли верхня планета видна після заходу Сонця в західній частині неба, вона переміщається серед зірок прямим рухом, тобто із заходу на схід, як і Сонце. Але кутова швидкість її руху менше, ніж у Сонця. Тому Сонце доганяє планету, і вона на якийсь час перестає бути видимою.

Незабаром, як тільки Сонце випередить планету, вона вже видна на сході перед сходом Сонця. Швидкість її прямого руху поступово зменшується, планета зупиняється, потім починає рух у зворотному напрямку - зі сходу на захід, причому її траєкторія нагадує петлю (мал. 9.2).

У середині дуги свого зворотного руху планета перебуває в сузір'ї, протилежному Сонцю; таке її положення називається протистоянням (мал. 9.1, положення М₃,).

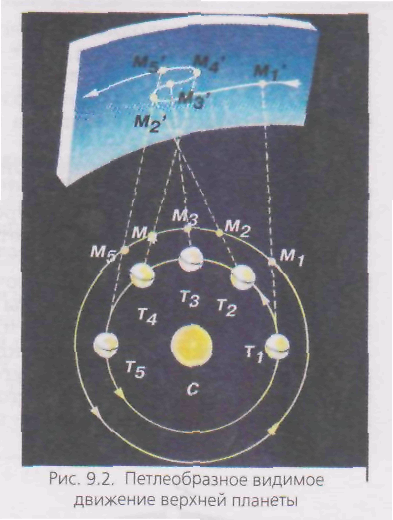
Через деякий час планета знову зупиняється, змінює напрямок свого руху на прямий, знову із заходу на схід. Незабаром її доганяє Сонце, вона перестає бути видимої - і весь цикл руху повторюється.

У середині дуги свого прямого руху, під час періоду невидимості, планета перебуває в тім же сузір'ї, що й Сонце. Таке її положення називається сполукою планети із Сонцем (мал. 9.1, положення М₃).

Розташування планети на 90^о на схід Сонця називається східною квадратурою, на 90^о на захід — західною квадратурою (мал. 9.1, положення відповідно М₄ і М₂).

Всі описані вище особливі положення планет щодо Сонця називаються конфігураціями.

Проміжок часу S між двома послідовними однаковими конфігураціями планети називається її синодичним періодом обігу. Для Меркурія він становить 116 діб, для Венери, Марса, Юпітера й Сатурна - відповідно 584, 780, 399 й 378 діб.

Особливості руху планет пов’язані з тим, що ми спостерігаємо їх із Землі, що також обертається навколо Сонця. Отже, петля в русі верхньої планети — це відображення руху Землі по орбіті. Тому чим далі планета, тим менше розмір її петлі. Так, ширина петлі зворотного руху Марса дорівнює 15^о, Юпітера – 10^о, Сатурна – 7^о.

2. Закони Кеплера. Використовуючи дані Птолемея, Н.Коперник визначив відносні відстані кожної планети від Сонця (у радіусах орбіти Землі), а також їх сидеричні (щодо зірок) періоди обігу навколо Сонця. Це дало можливість Йогану Кеплеру встановити три закони руху планет.

I. Кожна планета рухається навколо Сонця по еліпсу, в одному з фокусів якого перебуває Сонце.

Еліпс (мал. 9.3) — це замкнута крива, сума відстаней до кожної точки якої від фокусів F₁ і F₂ дорівнює його великій осі, тобто 2а, де а. — більша піввісь еліпса.

Якщо Сонце перебуває у фокусі F₁, а планета в точці Р, то відрізок прямої F₁P називається радіусом -вектором планети.

Відношення е = с/а, де c - відстань від фокуса еліпса до його центра, називається ексцентриситетом еліпса. Ексцентриситет визначає відхилення еліпса (ступінь його витягнутості) від окружності, для якої е = 0.

Орбіти планет у Сонячній системі дуже мало відрізняються від окружностей. Так, найменший ексцентриситет має орбіта Венери: е = 0,007; найбільший — орбіта Плутона: е = 0,249; ексцентриситет земної орбіти становить е = 0,0167.

Найближча до Сонця точка планетної орбіти П називається перигелієм, найбільш віддалена точка орбіти А — афелієм.

II. Радіус-вектор планети за однакові інтервали часу описує рівновеликі площі.

Із цього закону виходить важливий висновок: оскільки площі 1 й 2 (мал. 9.4) однакові, то по дузі Р_гР₂ планета рухається з більшою швидкістю, ніж по дузі Р₃Р₄, тобто швидкість планети найбільша в перигелії П и найменша — в афелії А.

III. Квадрати сидеричних періодів обертання планет від­носяться як куби великих півосей їхніх орбіт.

Якщо сидеричні періоди обертання двох планет позначити Т₁ і Т₂, а великі півосі їхніх орбіт — відповідно а₁ й а₂, то третій закон Кеплера буде мати вигляд

(9.1)

Закони Кеплера справедливі не тільки для планет, але й для їх природних і штучних супутників.

В 1687 р. І. Ньютон, вирішуючи завдання про взаємне притягання небесних тіл, точніше сформулював третій закон Кеплера для випадку, коли планета з масою М має супутник з масою т. Наприклад, для руху Землі навколо Сонця (сидеричний період Т_¤, піввісь орбіти а_¤.) і Місяця навколо Землі (відповідно Т_с й а_с третій закон Кеплера записується так:

(9.2)

Зневажаючи іншими додатками в дужках (їхні значення дуже малі в порівнянні з першими), можна визначити масу Сонця в одиницях маси Землі. У такий же спосіб визначають маси й інших небесних тіл, якщо вони мають природних або штучних супутників.

3. Рух штучних супутників Землі. Тут обговоримо деякі особливості руху штучних супутників Землі. У найпростішому випадку кругової орбіти супутника, якщо Н — його висота над поверхнею Землі й R — радіус Землі виражені в кілометрах, те його період обігу Т у хвилинах дорівнює

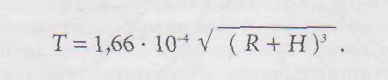
Наприклад, для висот Н = 220, 562 й 1674 км маємо період обігу відповідно Т = 89, 96 й 120 хв. Цікавий випадок, коли R = 35 800 км. Тоді Т = 23 ч 56 хв 4 з, а цей час, за яке Земля здійснює оборот навколо власної осі щодо зірок. Тому, якщо орбіта такого супутника лежить у площині земного екватора й він рухається в напрямку обертання Землі, то супутник увесь час буде перебувати «нерухомо над певною точкою земного екватора. Така орбіта називається геостаціонарною -

Найбільша відстань, перебуваючи на якій супутник усе ще буде обертатися навколо Землі, - 1,5 млн км. Якщо ж супутник виявиться на більшій відстані, то тяжіння з боку Сонця буде впливати на його рух, повертаючи супутник на менші висоти або ж перетворюючи його в штучну планету.

4. Рух космічних апаратів у просторі. Рух космічних апаратів (КА) у просторі описується тими ж законами, що й рух природних небесних тел.

Мінімальні енергетичні зусилля потрібні для запуску КА по напівеліптичній траєкторії, що називається гомановською (за іменем німецького вченого В. Гомана).

Тривалість польоту КА t_ка можна визначити за третім законом Кеплера. Оскільки сидеричний період обігу КА Т_кв навколо Сонця по цій орбіті дорівнював би

то

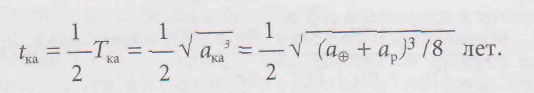
Таким чином, знаходимо, що політ КА до Венери триває 146 доби, а до Марса - 259 доби.

З огляду на те, що кутові швидкості руху Венери, Землі й Марса по орбітам відповідно рівні 1,6^о, 1^о й 0,52° у добу, можемо одержати взаємні положення планет на момент старту КА із Землі (мал. 9.5): Венера на кутовій відстані 54 ^о, а Марс — на 44° спереду Землі. Коли КА виявиться біля Венери, Земля буде перебувати на 36" за нею, а в момент зустрічі КА з Марсом - на 75^о поперед нього.

Отримані рішення використають і при визначенні тривалості очікування сприятливого розташування Венери або Марса для повернення КА на Землю. Це може здійснитися тільки за таких умов: від Венери — коли Земля виявиться на кутовій відстані 36^о поперед неї; від Марса — коли Земля буде перебувати на 75^о за ним. У результаті обчислень знайдено, що згадане очікування сприятливого розташування планет Венери й Землі триває 480 діб, Марса й Землі - 438 діб.

Отже, загальна тривалість експедиції до Венери з поверненням на Землю дорівнює 770 діб, до Марса - 956 діб.

1. По яким особливостям видимого руху планети поділяються на верхні і нижні?

2. Що таке конфігурація планет?

3. Що таке синодичний та сидеричний періоди обігу планет?

4. Що таке радіус-вектор планети?

5. Як «зважують» небесні тіла?

6. За скільки діб штучний супутник робить повний оборот навколо Землі, якщо він знаходиться на відстані 1,5 млн км?

9.1. Використовуючи «Астрономічний календар», прослідкуйте зміни положення на небі однієї-двох планет на протязі року, встановіть дати їх конфігурацій, якщо такі в цьому році траплялися.

9.2. Перевірте правильність даних про тривалість очікування КА біля Венери і Марсу для успішного повернення на землю.