§ 8. Производящие функции рекуррентных последовательностей

1. Алгебра формальных рядов

Определение 8.1. Формальным рядом назовем степенной ряд

,

где  элементы поля .

Два формальных ряда называются равными, если равны их коэффициенты при одинаковых степенях .

Сумма формальных рядов и определяется следующим образом: .

Операция умножения формального ряда на скаляр из поля  определяется соотношением: .

Введенные таким образом операции задают на множестве  формальных рядов структуру бесконечномерного векторного пространства.

Произведение формальных рядов определяется как формальный ряд условием:

.

Коэффициент при вычисляется по формуле:

.

Векторное пространство формальных степенных рядов с введенной операцией умножения рядов становится линейной алгеброй над полем , которая называется алгеброй формальных рядов. Заметим, что эта алгебра ассоциативна, коммутативна и обладает единицей. Единица имеет вид: , где 1  единица поля .

Определение 8.2. Формальный ряд называется обратимым, если существует степенной ряд такой, что .

Предложение 8.1. Формальный ряд обратим тогда и только тогда, когда .

Доказательство. 1. Пусть – обратный ряд. Тогда существует , причем

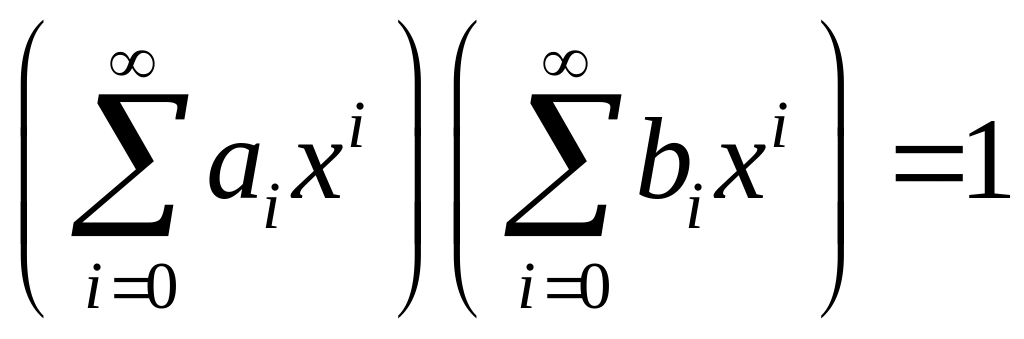. (8.1)

Левую часть можно представить в виде формального ряда , где

, (8.2)

причем при , , а .

При получаем

. (8.3)

Из равенства формальных рядов следует, что , поэтому . Следовательно, .

2. Пусть . Составим соотношение (8.1), где коэффициенты ряда подлежат определению. Из равенства (8.3) в силу , следует, что .

Предположим . Вычислим . По формуле (8.2) найдем :

.

Отсюда, учитывая, что , найдем :

.

Таким образом, формальный ряд , удовлетворяющий условию (8.1), существует.

2. Определение производящей функции рекуррентной последовательности

Рассмотрим рекуррентную последовательность над полем , удовлетворяющую соотношению , . Первые членов последовательности будем считать фиксированными.

Определение 8.3. Формальный ряд называется производящей функцией рекуррентной последовательности .

Пример.  производящая функция последовательности чисел Фибоначчи.

3. Нахождение производящей функции рекуррентной последовательности

Пусть – рекуррентная последовательность, удовлетворяющая соотношению

и пусть через производящая функция этой последовательности. Поставим задачу получения способа построения . Из определения производящей функции имеем

. (8.4)

Умножим равенство (8.4) последовательно на 1, , , …, , и затем полученные равенства сложим. Коэффициенты при имеют вид

поэтому все они равны нулю. Следовательно, после сложения рассматриваемых равенств, получим следующее равенство:

,

где – многочлен степени , коэффициенты которого вычисляются по формулам:

,

,

, (8.5)

.

Многочлен является двойственным характеристическому многочлену . Таким образом, производящая функция получается при деление многочлена на :

.

Многочлен называется производящим многочленом рекуррентной последовательности. Полученный результат сформулируем в виде теоремы.

Теорема. Пусть – однородная рекуррентная последовательность порядка над полем , – характеристический многочлен, – двойственный многочлен, – производящая функция этой последовательности. тогда имеет место равенство:

, (8.6)

где ,а вычисляются по формулам (8.5).

Верно и обратное утверждение: если – многочлен степени , задается равенством , то формальный степенной ряд , задаваемый равенством (8.6), является производящей функцией некоторой однородной рекуррентной линейной последовательности, характеристический многочлен которой определяется условием .

Формулам (8.4) можно придать другой вид. Для этого введем матрицу

,

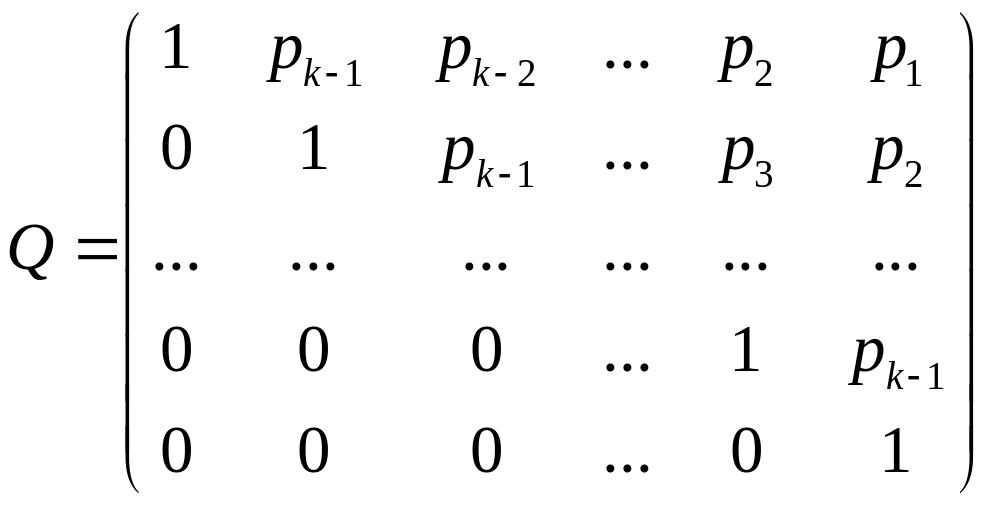строками которой являются коэффициенты характеристического многочлена: первая строка составлена из коэффициентов характеристического многочлена отбрасыванием коэффициента , каждая другая строка получается из предыдущей отбрасыванием последнего элемента и добавлением нуля слева от главной диагонали. Умножив начальный вектор однородной линейной последовательности на матрицу получим вектор :

.

Пример. 1. Найдем производящую функцию для последовательности чисел Фибоначчи.

Члены последовательности Фибоначчи удовлетворяют соотношению .

Составим характеристический многочлен . Двойственным для него будет многочлен .

Коэффициенты многочлена найдем по формуле , где , .

.

Следовательно, . Получим производящую функцию :

_ 1 1  х  х²

1  х  х² 1 + х + 2х² + 3х³ + …

_ х + х²

х  х²  х³

_2х² + х³

2х²  2х³ 2х⁴

_3х³ + 2х⁴

3х³  3х⁴ 3х⁵

5х⁴ 3х⁵

…

.

Задачи

1. Пусть ,  формальные ряды над полем . Найдите произведение этих рядов над данным полем.

2. Найдите ряд, обратный над полем .

3. Найдите производящую функцию рекуррентной последовательности, удовлетворяющей соотношению , , над полем .

4. Найдите производящую функцию для последовательности, удовлетворяющей рекуррентному соотношению , , , над полем . Определите период этой последовательности.

5. Найдите производящую функцию для рекуррентной последовательности , , над полем .

Указание. Повысив порядок рекуррентности, перейдите к однородному соотношению.

6. Найдите производящую функцию последовательности, удовлетворяющей соотношению , , , .

7. Найдите производящую функцию для рекуррентной последовательности , , над полем .

8. Докажите, что каждая линейная рекуррентная последовательность порядка k над полем  характеристики q является периодической. При этом ее минимальный период r (наименьший из всех возможных периодов) удовлетворяет условию:

а) , если последовательность неоднородная;

б) , если последовательность однородная.

9. Разложить в степенной ряд по возрастающим степеням дробь

.

10. Найти однородное линейное рекуррентное уравнение, которому удовлетворяют коэффициенты разложения дроби задачи 9.