§4. Дифференциальные операторы специального типа в алгебре многочленов

При решении рекуррентных уравнений полезным является дифференциальные операторы специального вида.

В алгебре многочленов  определим операцию   по правилу

.

Операция -линейна. Действительно, для произвольных  и , имеем

,

.

Кроме того, является дифференцированием алгебры многочленов  :

Предложение 4.1. Дифференцирование удовлетворяет равенствам:

(а)

(б)

Доказательство. (а). Так как , то . Отсюда следует (а).

(б). Из определения следует, что

.

Утверждение доказано.

Определим по индукции операции   :

,

.

Предложение 4.2. Имеет место тождество:

Доказательство проведем методом математической индукции по

1. При имеем

.

2. Пусть утверждение верно для фиксированного :

.

3. Проверим справедливость равенства для :

.

Утверждение доказано.

Предложение 4.3. -линейный оператор на  .

Доказательство проведем методом математической индукции.

1. При оператор – -линейный.

2. Пусть – -линейный оператор.

3. Докажем, что оператор -линейный. Для произвольных  и   имеем:

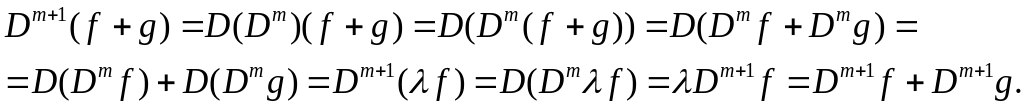
Следствием предложений 4.1 – 4.3 является

Предложение 4.4. Для произвольного многочлена имеют место равенства:

(при ).

Предложение 4.5. Для произвольного натурального числа и произвольного многочлена  выполняются равенства:

где некоторые элементы поля , а – произвольные многочлены .

Доказательство.

1. При равенство выполняется по определению оператора :

.

2. Предположим, что утверждение верно при , для произвольного фиксированного : где – некоторые скаляры из .

3. Докажем справедливость утверждения при . Из определения оператора и предложения 1 получим:

, .

Утверждение доказано.

Предложение 4.6. Пусть , . Если , то и .

Доказательство. 1. Проверим, что утверждение верно при . Пусть . Тогда и . То есть утверждение верно при .

2. Предположим, что утверждение верно при .

3. Докажем истинность утверждения при . Пусть для . В силу индуктивного предположения имеем и . Но , поэтому . На основании предложения 4.5 можно записать следующее равенство:

.

Отсюда следует, что . Предложение 4.6 доказано.

Предложение 4.7. Пусть  – поле нулевой характеристики. Следующие условия для  , логически эквивалентны:

(1) -кратный корень многочлена   ;

(2) и .

Доказательство. Докажем истинность импликации . Пусть -кратный корень. Тогда из курса алгебры известно, что:

и .

Тогда . Из предложения 4.5 при получим:

и .

Истинность импликации доказана.

Пусть выполняется условие (2). Тогда из предложения 4.5 получаем, что

и .

Отсюда следует, что -кратный корень многочлена   . Истинность импликации доказана.

§5. Решение линейных однородных рекуррентных уравнений в случае различных кратных корней характеристического уравнения

В этом параграфе будем исследовать решения линейного однородного уравнения (3.1) в случае, когда среди корней есть кратные корни. Будем считать, что характеристика поля  равна нулю.

Теорема 5.1. Если -кратный корень характеристического многочлена рекуррентного уравнения (3.1), то последовательность является решением уравнения (3.1).

Доказательство. При утверждение следует из предложения 3.1.

При запишем результат подстановки последовательности в левую часть уравнения (3.1):

. (5.0)

По формуле бинома Ньютона

,

при равенство (5.0) перепишем следующим образом:

.

Так как для , то полученное выражение тождественно равно нулю. Теорема 5.1 доказана.

Теорема 5.2. Пусть попарно различные корни характеристического многочлена рекуррентного уравнения (3.1) и пусть кратности этих корней равны , соответственно. Тогда система решений

линейно независима.

Доказательство. Составим линейную комбинацию этих решений и приравняем нулю. Тогда получим тождество относительно :

(5.1)

Придадим переменной значения 0, 1, 2, …, k–1. Тогда из тождества (5.1) получим систему:

(*),

Матрица этой системы будет следующей:

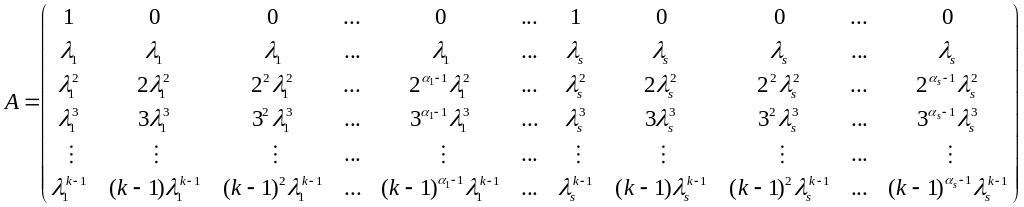
Докажем, что . Доказательство проведем от противного. Предположим, что . Тогда система строк этой матрицы линейно зависима. Значит, существуют скаляры , не равные нулю одновременно, такие, что

,

где – строки вещественной матрицы .

Значит,

(5.2)

Координаты каждого вектора можно разбить на блоков, соответствующих корням .

Из равенства (5.2) следует аналогичные равенств для соответствующих координат векторов системы .

Выпишем равенства для блока, соответствующего корню

(5.3)

.

Рассмотрим многочлен

.

Равенства (5.3) в силу предложения 4.4 примут вид:

Отсюда замечаем, что кратность корня многочлена не меньше, чем : . Напомним, что -кратность корня характеристического многочлена.

Оценим число корней многочлена . Как было установлено выше, кратности корней соответственно многочлена удовлетворяют неравенствам .

Поэтому . С другой стороны, – степень характеристического многочлена.

Следовательно, число корней многочлена равно .

Степень многочлена не превосходит , поэтому имеет не более, чем корней. Это значит, . Отсюда . Получили противоречие. Следовательно, система строк имеет ранг, равный . Поэтому система (*) имеет единственное нулевое решение. Значит,

, .

Теорема доказана.

Из доказанных теоремы 5.1 и теоремы 5.2 следует

Теорема 5.3. Если различные корни характеристического многочлена однородного рекуррентного уравнения (3.1), кратности корней равны , соответственно, то каждое решение уравнения (3.1) можно представить в виде

,

где , – многочлен степени не больше, чем , коэффициенты которого однозначно определяется начальными условиями и принадлежат полю разложения характеристического многочлена над .

Замечание. Теорема 5.3 имеет место и в случае, когда поле  имеет конечную характеристику , при условии, что кратности корней характеристического уравнения меньше, чем .

Задачи

Решить следующие рекуррентные уравнения

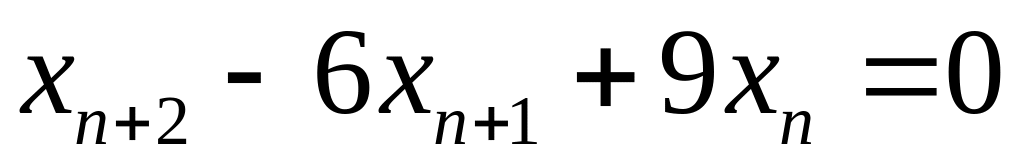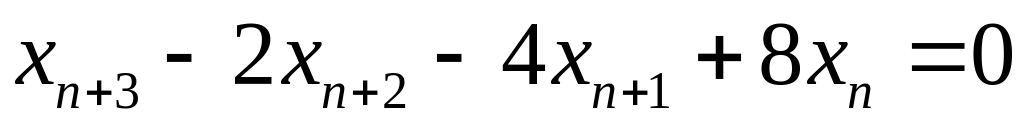1. .

2. .

3. .

4. .