1.Сущность теплопроводности. Температурное поле, его характеристики, градиент температуры, его знак и направленность.

Различают три способа распространения теплоты в природе – теплопроводность, конвекцию и тепловое излучение и два вида теплообмена между телами – конвективный и лучистый.

Процесс распространения теплоты теплопроводностью является молекулярным процессом и происходит при непосредственном соприкосновении тел или частиц тел с различной температурой. В результате соударения частиц вещества( молекул, атомов и св. электронов) происходит обмен энергией их теплового движения: интенсивность движения частиц тела, обладающих меньшей внутренней кинетической энергией, увеличивается, а частиц тела, обладающих большей внутренней кинетической энергией, уменьшается.

Механизм распространения теплоты теплопроводностью зависит от физ. свойств тела: в газообразных тела перенос теплоты теплопроводностью происходит в результате соударения молекул между собой; в металлах – путем диффузии свободных электронов; в капельных жидкостях и твердых телах-диэлектриках – путем упругих волн( упругие колебания крист. решетки)

Для возникновения процесса теплопроводности необходимо наличие разности температур в различных точках среды. Совокупность значений температуры в данный момент времени для всех точек рассматриваемой среды называется температурным полем. В общем случае уравнение температурного поля имеет вид : t=f(x, y, z, τ), где t-температура среды; x, y, z – координаты точки среды; τ-время.

В том случае, когда температура зависит от времени, температурное поле называется нестационарным. Если температура в любой точке среды не зависит от времени, то температурное поле называется стационарным и описывающее его уравнение имеет вид: t=f(x, y, z). Для такого поля .Поскольку температура величина скалярная – то температурное поле скалярное.

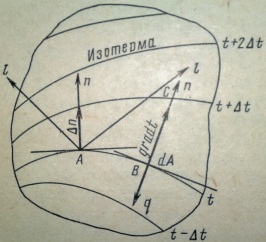
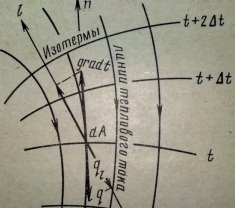
Рис.1 Рис.2

Геометрическое место точек, имеющих в данным момент времени одинаковую температуру, называется изотермической поверхностью. Уравнение изотермической поверхности

f(x, y, z, τ)=const.

При нестационарном температурном поле изотермические поверхности с течением времени меняют своё положение в пространстве. При стационарном температурном поле уравнение изотермической поверхности будет f(x, y, z)=const и ее вид и расположение в теле остаются не зависящими от времени. На рис 1 схематически изображено сечение тела с нанесенными через интервалы Δt изотермами( линии пересечении изотермических поверхностей с плоскостью чертежа). Вдоль всякого направления l, несовпадающего с изотермой, температура изменяется. Наименьшее расстояние между двумя изотермическими поверхностями имеет место в направлении нормали n к изотермической поверхности( т. А на рис1)