1. Понятие и представление комплексных чисел.

Комплексные числа являются расширением множества действительных чисел. В результате расширения множества действительных чисел было введено понятие мнимой единицы  , которая существует на множестве комплексных чисел, но не существует на множестве действительных. Мнимая единица удовлетворяет равенству:

.

(1)

В литературе часто мнимую единицу обозначают через  . Тогда комплексное число  можно представить в виде:

,

(2)

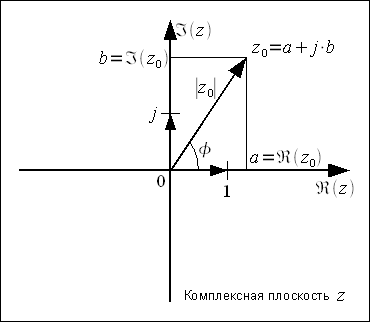
где   носит название действительной части или реальной части и обозначается  , а  носит название мнимой части и обозначается как  . Графически все множество действительных чисел можно представить на бесконечной числовой прямой, при этом комплексные числа можно трактовать как расширение числовой прямой до комплексной плоскости, а каждое комплексное число можно представить как точку на комплексной плоскости (смотри рисунок 1). При этом все множество действительных чисел будет представляться прямой на комплексной плоскости.

2. Рисунок 1: Представление комплексного числа на плоскости

Комплексная плоскость   делится прямыми реальной части   (прямой действительных чисел) и прямой мнимых чисел  на четыре четверти. Любое комплексное число   ,будет представляться точкой на комплексной плоскости с координатами   и  . Если число не содержит мнимой части, то оно действительное и находится на прямой , а если число не содержит реальной части, то оно называется чисто мнимым и находится на оси  .

Модуль и фаза комплексного числа

Если из начала координат комплексной плоскости к точке   восстановить вектор, то можно вычислить длину этого вектора как

.

(3)

При этом   — действительное число характеризующее длину вектора и называется модулем комплексного числа. При этом сам вектор комплексного числа повернут относительно оси   на некоторый угол  , называемый фазой. Связь реальной и мнимой частей комплексного числа с его амплитудой и фазой представлено следующим выражением:

(4)

Тогда комплексное число можно представить в тригонометрической форме

.

(5)

Связь угла поворота вектора комплексного числа с реальной и мнимой частью комплексного числа:

,

(6)

тогда

,

(7)

где   учитывает четверть комплексной плоскости в которой расположено число  :

.

(8)

Функция которая позволяет получить угол   c учетом четверти комплексной плоскости в которой расположен вектор называется функция арктангенс-2 и обозначается  . Функция арктангенс-2 присутсвует во всех математических приложениях и может быть использована для расчета верного угла поворота вектора комплексного числа.

Показательная форма комплексного числа. Формула Эйлера

Существует также показательная форма комплексного числа связанная с тригонометрической по формуле Эйлера:

.

(9)

Данное соотношение легко доказать, если произвести разложение экспоненты в ряд Тейлора:

.

(10)

Представим ряд в виде суммы четных и нечетных членов последовательности:

.

(11)

Рассмотрим более подробно мнимую единицу в четной и нечетной степенях. Выражение (1) задало  , тогда , в свою очередь  . Таким образом можно рекурентно записать:

.

(12)

Построим аналогичным облразом рекурентное соотношение для нечетных степеней:  тогда  , в свою очередь  , получим:

.

(13)

Таким образом выражение (11) с учетом (12) и (13) принимает вид:

.

(14)

В выражении (14) первая сумма по четным степеням дает разложение в ряд Тейлора функции косинуса, а вторая сумма по нечетным степеням дает разложение в ряд Тейлора функции синуса. Таким образом, получено доказательство справедливости формулы Эйлера (9). Используя формулу Эйлера можно сделать ряд важных замечаний: Замечание 1:

.

(15)

Замечание 2:

.

(16)

Операции над комплексными числами. Сложение комплексных чисел

Сумма двух комплексных числел   и   есть также комплексное число  :

.

(17)

Как следует из выражения (17) при сложении реальные и мнимые части комплексного числа также складываются.

На комплексной плоскости операцию сложения можно реализовать как сложение векторов комплексных чисел по правилу параллелограмма (рисунок 3).

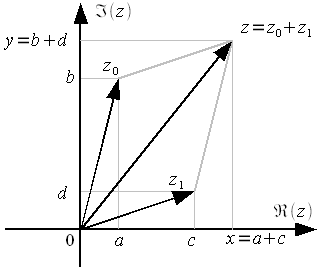3. Рисунок 3: Сложение комплексных чисел

Операции над комплексными числами. Вычитание комплексных чисел

Разность двух комплексных числел  и   есть также комплексное число  :

.

(18)

Как следует из выражения (18) при вычитании реальные и мнимые части комплексного числа также вычитаются.

На комплексной плоскости операцию вычитания можно реализовать как вычитание векторов комплексных чисел по правилу параллелограмма (рисунок 4). На первом шаге из вектора   формиуется вектор   после чего вектор   складывается с вектором   по правилу параллелограмма.

Операции над комплексными числами. Умножение комплексных чисел

Для того чтобы получить формулу для умножения комплексных числен необходимо перемножить два комплексных числа по правилу умножения многочленов:

(19)

Таким образом получили также комплексное число. Умножать в явном виде комплексные числа не очень удобно, гораздо проще если привести их по формуле Эйлера к показательной форме:

.

(20)

При перемножении в показательной форме модули комплексных числел перемножаются а фазы складываются. На векторной диаграмме это можно представить следующим образом (рисунок 5):

При перемножении результирующий вектор поворачивается и его длина изменяется.

Исходя из выражения (15), умножение комплексного числа на чисто мнимое число приводит к повороту вектора на 90 градусов против часовой стрелки (к фазе   прибавляется 90 градусов). При этом из выражения (16) следует что умножение комплексного числа на -1 приводит повороту фазы на угол 180 градусов (вектор отражается относительно 0). Это очень важное замечание, так как емкости и индуктивности имеют чисто мнимые сопротивления и служат для поворота вектора комплесного сигнала, в то же время поворот фазы на 180 градусов позволяет сформировать фазоманипулированные сигналы.

Комплексно-сопряженные числа

Необходимо сделать еще одно замечание: числа   и   называются комплексно-сопряженными. При этом комплексно-сопряженное число обозначается чертой   Согласно выражениям (3) и (7) их модули равны, а фазы равны по модулю но имеют противоположные знаки:

.

(21)

Произведение согласно выражению (19) равно:

.

(22)

Таким образом произведение комплексно-сопряженных чисел есть действительное число равное квадрату модуля этих чисел. Векторное представление комплексно-сопряженных чисел представлено на рисунке 6.

Операции над комплексными числами. Деление комплексных чисел

Последняя операция которую осталось рассмотреть — операция деления комплексных чисел. Рассмотрим деление в показательной форме:

(23)

Таким образом при делении комплексных чисел их модули делятся а фазы вычитаются. При делении необходимо чтобы . Получим формулу для деления комплексных чисел в явной форме. Пусть

(24)

умножим и числитель и знаменатель дроби на число комплексно-сопряженное знаменателя:

.

(25)

Исходя из (22) в знаменателе дроби получим квадрат модуля знаменателя а числитель перемножим по правилу умножения комплексных чисел:

.

(26)

Поделив почленно реальную и мнимую часть числителя на знаменатель получим:

.

(27)

Выражение (27) - формула деления комплексных чисел в явной форме. Как можно заметить операции сложения и вычитания удобнее выполнять в явном виде, тогда как умножать и делить комплексные числа быстрее и легче в показательной форме.

2. Действия над комплексными числами.

3. Ряды Фурье.

Ряд Фурье — в математике — способ представления произвольной сложной функции суммой более простых. В общем случае количество таких функций может быть бесконечным, при этом чем больше таких функций учитывается при расчете, тем выше оказывается конечная точность представления исходной функции. В большинстве случаев в качестве простейших используются тригонометрические функции синусаи косинуса, в этом случае ряд Фурье называется тригонометрическим, а вычисление такого ряда часто называют разложением на гармоники.

Классическое определение 

Тригонометрическим рядом Фурье называют функциональный ряд вида

или, более сжато

(1)

Постоянные числа  ,   и   ( ) называются коэффициентами тригонометрического ряда.

Если ряд (1) сходится, то его сумма есть периодическая функция   с периодом  , так как   и   являются периодическими функциями с периодом  .

Общее определение 

Пусть в Гильбертовом пространстве   даны ортогональная система   и   — произвольный элемент из  . Последовательность чисел

называется координатами, или коэффициентами Фурье элемента   по системе  , а ряд

называется рядом Фурье элемента   по ортогональной системе  .

Справедливо т. н. неравенство Бесселя:

Если выполнено равенство Парсеваля

,

то нормированная система   называется замкнутой.

Справедливо утверждение: в сепарабельном евклидовом пространстве   всякая полная ортогональная нормированная система является замкнутой и наоборот.

Сходимость ряда Фурье 

Теорема: Шаблон:Начало цитаты Если периодическая функция   с периодом   — кусочно-монотонная[1] и ограниченная на отрезке  , то тригонометрический ряд Фурье, построенный для этой функции, сходится во всех точках. Сумма полученного ряда   равна значению функции   в точках ее непрерывности. В точках разрыва   сумма ряда равняется среднему арифметическому пределов функции   справа и слева. Шаблон:Конец цитаты

Из этой теоремы следует, что тригонометрические ряды Фурье применимы к достаточно широкому классу функций.

4.Функции двух переменных.

Если указано правило, согласно которому с каждой точкой М плоскости (или какой-нибудь части плоскости) сопоставляется некоторое число u, то говорят, что на плоскости (или на части плоскости) «задана функция точки»; задание функции символически выражается равенством вида u=f(M). Число u, сопоставляемое с точкой М, называется значением данной функции в точке М. Например, если А - фиксированная точка плоскости, М - произвольная точка, то расстояние от А до М есть функция точки М. В данном случае f(m)=AM.

Пусть дана некоторая функция u=f(M) и вместе с тем введена система координат. Тогда произвольная точка М определяется координатами x, y. Соответственно этому и значение данной функции в точке М опеределяется координатами x, y, или, как еще говорят, u=f(M) есть функция двух переменных x и y. Функция двух переменных x и y обозначается символом f(x; y): еслиf(M)=f(x;y), то формула u=f(x; y) называется выражением данной функции в выбранной системе координат. Так, в предыдущем примере f(M)=AM; если ввести декартову прямоугольную систему координат с началом в точке А, то получим выражение этой функции:

.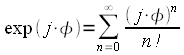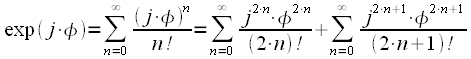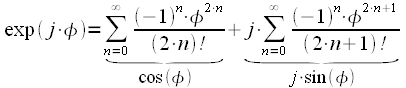