Структура автоматизированной обучающей системы

В начале студент попадает на страницу регистрации, где он указывает свои личные данные: фамилию, группу, номер зачетки. Далее программа производит поиск студента с такими данными в списке студентов, проверяет наличие допуска к тестированию.

Вторым этапом является подготовка к тесту, на котором студент вводит полученные на предыдущем шаге данные в форму начала теста.

Третий этап - непосредственно тестирование. Студенту будет предложен ряд вопросов, на которые он должен дать ответы. Каждый вопрос может содержать как один так и несколько правильных ответов на поставленный вопрос.

На каждый вопрос ему отводится 1 минута, по истечении времени вопрос не зачитывается и задается следующий. За 10 секунд до окончания времени выдается предупреждение.

Четвертый этап - завершение тестирования. Студенту и преподавателю автоматически системой выдаются результаты тестирования. Сам результат сохраняется и в базе деканата.

За ведение базы студентов отвечает ответственный преподаватель. Система является автоматизированной и сама создает запросы на выборку сведений о студентах (успеваемость - из базы деканата). Программа сама контролирует на каком курсе учится студент и в соответствии с этим выдает ему базу вопросов, соответствующую его уровню знаний.

2.2.2 Разработка методов решения задач

Студенту предлагается несколько вопросов из общей совокупности некоторого раздела изучаемого курса. Выбирают вопросы случайным образом. Число вопросов может варьироваться в зависимости от степени правильности ответов на предыдущие вопросы. Все вопросы подразделяются на несколько категорий сложности. Самая верхняя категория - самые сложные вопросы. Вес вопроса из этой категории составляет единицу. В случае если тестирующийся правильно отвечает на предложенный вопрос из данной категории, то следующий вопрос ему будет задан из этой же категории сложности. В этом случае весь тест будет состоять всего лишь из нескольких сложных вопросов.

Если же тестирующийся отвечает неправильно на поставленный вопрос, то следующий вопрос будет ему предложен из более легкой категории, но одному вопросу из первой категории будут сопоставлены несколько вопросов второй.

Сущность статистического способа оценки знаний заключается в следующем: составляется программа из N контрольных вопросов. Для каждого студента выбирается n вопросов. Определяется число m правильных ответов. В зависимости от доли правильных ответов δ=m/n принимается решение о выборе j-той оценки, j=1,k. Здесь величина k определяет максимальное число баллов по принятой шкале оценок. При k=2 шкала оценок соответствует двухбалльной оценке: «Зачет», «Незачет».

Таким образом, при чисто статистическом подходе оценка качества знаний сводится к определению вероятности получения m правильных ответов на случайную выборку n вопросов из N. Если принять гипотезу, что студент сможет ответить на М вопросов из N, то такая вероятность определяется выражением:

Р(n, m)= С^m_MCⁿ_N^-_-^m_M/Cⁿ_N

где Cⁿ_N – число сочетаний из М по m.

Качество навыков оценивается по скорости и точности выполнения требуемых операций. При достаточно большом времени наблюдений скорость выполнения операции:

_n

С= n/∑τ_i

ⁱ⁼¹

где τ_i – время выполнения операции на i-той попытке;

n – количество попыток.

Более удобно оценивать уровень владения операцией по среднему времени ее выполнения:

_n

τ_ср = ∑τ_i/ n

ⁱ⁼¹

Такая оценка удобнее не только при итоговом контроле, но и в процессе тренировочных упражнений. Дисперсия величины τ определяется выражением:

_n

s²_τ = ∑(τ_i-τ)/ n

ⁱ⁼¹

, n>1.

Для АОС удобнее пользоваться следующим выражением:

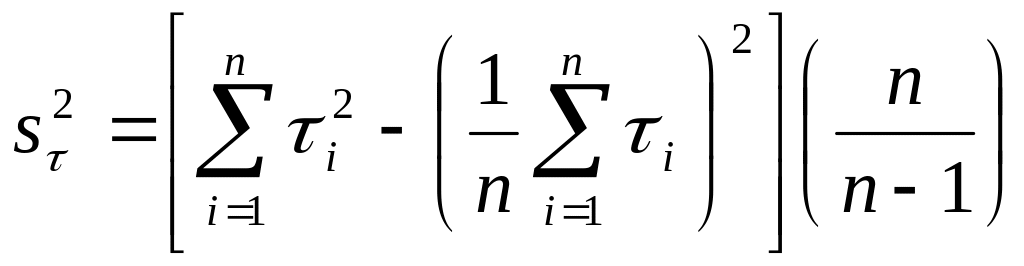
При n>1 сомножителем можно пренебречь. Средняя квадратическая ошибка величины τ будет:

В ряде случаев целесообразно пользоваться относительными показателями качества владения умениями. Относительная скорость выполнения операции:

_n

ν = nτ_доп/ ∑τ_i

ⁱ⁼¹

Относительная успешность действий:

ξ=Р/Р_н

С математической точки зрения задача автоматизированного управления обучением может рассматриваться как задача дискретного управления многошаговым процессом с заданным конечным состоянием s_к и набором допустимых действий D, таких, что действие d_i є D, реализуемое на i-том шаге, переводит обучаемого из состояния s_i в состояние s_i+1. в обучающих программах состоянию обучаемого соответствует описание его знаний. В этом случае задача управления обучением состоит в выборе оптимальной последовательности состояний s^*=< s₀, s^*₁, s^*₂, …> и действий d^*=< d^*₀, d^*₁, d^*₂, …>, таких, что достигается минимальное значение показателя качества обучающей системы – времени обучения:

Т(s^*, d^*)=min T(s₀, s_k,d_j),

где s₀ – начальное, s_k – желаемое состояние знаний обучаемого;

d_j - последовательность действий обучающей программы;

j – номер допустимой последовательности.

По принципу управления программы, моделирующие действия преподавателя, делятся на программы прямого управления и циклические. По принципу прямого управления работают программы, реализующие демонстрационный метод обучения. Циклические программы подразделяются по виду целевой функции. В соответствии с характером изменения целевой функции (нормы регулирования) можно выделить следующие виды управления: программное, следящее, адаптивное и экстремальное.

При программном управлении цель определяется функцией времени

g=f_n(t). К такому виду относится большинство программ традиционного программного обучения.

Следящему управлению соответствует целевая функция g=f_с(W), где W - некоторая ведущая величина. К этому виду можно отнести программы, обучающие действиям, воспроизводящим функционирование некоторой эталонной модели (например, вычислителя).

При адаптивном управлении текущая цель выбирается на основе анализа состояний обучаемого в предшествующие моменты времени:

g(t_i)=f_a[y(t₀), y(t₁), …, y(t_i-1)]

Такую схему управления имеют самоприспосабливающиеся программы. первым приближением к адаптивным обучающим программам можно считать настраиваемые программы, т.е. такие, в которых контур адаптации реализуется с помощью преподавателя. В случае использования в схеме управления моделей процесса обучения и деятельности обучаемого можно говорить о реализации рефлексивного управления. Схема рефлексивного управления принципиально отличается от других схем наличием описаний деятельности управляемого и управляющего объектов.

При экстремальном управлении выбор текущих целей определяется последовательностью состояний, на которой показатель качества достигает экстремального значения. Например, экстремальная задача АОС может состоять в минимизации времени обучения заданной системе понятий или в максимизации знаний обучаемого за заданное время.

При нормативном подходе к организации учебного процесса (например при строго определенном критерии достижения цели обучения и ограниченном времени обучения) задача повышения эффективности сводится к поиску системы с минимальной стоимостью, т.е. требуется решить задачу:

_n

∑С_i(z⁰_i,T_i)→min;

ⁱ⁼¹

z_i(z⁰_i, T_i)≥z_н; i=1,n;

T_i≤T_д

где С_i – стоимость (обобщенная) обучения i-го студента;

z_i, z⁰_i, z_н – текущие, начальные и необходимые знания i-го студента;

T_i, T_д – затраченное и допустимое время обучения;

n – число обучаемых.

Более близкой к реальности представляется задача типа:

_n

∑z_i(z⁰_i,T_i)→max;

ⁱ⁼¹

z_i(z⁰_i, T_i)≥z_н; i=1,n;

T_i≤T_д;

_n

∑С_i(z⁰_i,T_i)≤C_д

ⁱ⁼¹

где С_i – стоимость обучения i-го студента;

C_д – допустимые затраты.

Это задача передачи максимума знаний при ограниченных ресурсах.

Во всех приведенных формулировках задач содержится величина z_i – объем или степень усвоения знаний, которая в настоящее время не имеет точной меры. таким образом, задача оптимизации процесса обучения содержит в своих условиях неопределенность. В связи с этим в формулировку задачи вводятся случайные величины, принимающие значения 1(знает) и 0(не знает) с некоторой вероятностью. Тогда последняя задача принимает вид:

_n

∑δ_i(z⁰_i,T_i)→max;

ⁱ⁼¹

δ_i≥δ_д;

_m

δ_i=∑р_ij(z⁰_i, T_i)δ^j;

^j=1

_m

∑р_ij(z⁰_i, T_i)=1;

^j=1

T_i≤T_д;

_n

∑С_i≤C_д

ⁱ⁼¹

где δ_i – степень знаний обучаемого i, достигнутая за время T_i;

р_ij – вероятность того, что i-й обучаемый за время T_i может получить оценку δ^j.

В таблице 2.2.1 приведены обозначения, используемые в математической модели.

Таблица 2.2.1

№	Обозначение	Наименование и пояснения	Размерность
1	2	3	4
1.	i	№ студента
2.	j	№ уровня сложности
3.	n	Количество студентов
4.	m	Количество уровней сложности
5.	δi	Степень знаний обучаемого i, достигнутая за время Ti	i=1,n
6.	z0i	Начальные знания i-го студента	i=1,n
7.	Ti	Затраченное время обучения	i=1,n
8.	δд	Степень допустимых знаний студентов
9.	δj	Оценка	j=1,m
		Продолжение таблицы 2.2.1
10.	рij	Вероятность того, что i-й обучаемый за время Ti может получить оценку δj	i=1,n; j=1,m
11.	Tд	Допустимое время обучения
12.	Сi	Стоимость обучения i-го студента	i=1,n
13.	Cд	Допустимые затраты

Целевая функция:

_n

∑δ_i(z⁰_i,T_i)→max; где i=1,n. (1)

ⁱ⁼¹

Ограничения задачи:

δ_i≥δ_д; где i=1,n; (2)

_m

δ_i=∑р_ij(z⁰_i, T_i)δ^j; где i=1,n; j=1,m; (3)

^j=1

_m

∑р_ij(z⁰_i, T_i)=1; где i=1,n; j=1,m; (4)

^j=1

T_i≤T_д; где i=1,n; (5)

_n

∑С_i≤C_д где i=1,n; (6)

ⁱ⁼¹

Найти значения переменных δ_i (i=1,n), обеспечивающих максимум целевой функции (1) при ограничениях (2-6).