ГБОУ ВПО КГМУ

Зав. кафедрой физики,

информатики и математики,

доцент Снегирева Л. В.

Самостоятельная работа №1

Тема: «Корреляционный и регрессионный анализ».

Выполнила:

студентка лечебного

факультета, 1 курса, 23 группы

Дубовская Дарья Сергеевна.

Проверила:

асс. Новичкова Т.А.

Курск 2012

План

1. Введение………………………………………………………………..стр.3

2. Понятие корреляции. Корреляционный анализ и его основы. Составление корреляционных таблиц…………………………….стр. 4-8

3. Выборочное уравнение линейной регрессии Y на X и X на Y….стр.9-10

4. Коэффициент линейной корреляции и его свойства……………….стр.11

5. Проверка гипотезы о значимости выборочного коэффициента линейной корреляции……………………………………………..стр.12-15

6. Заключение……………………………………………………………стр.16

7. Список литературы…………………………………………………...стр.17

Введение

При изучении зависимостей между величинами важным является рассмотрение не только функциональных, но и статистических зависимостей, наиболее важной и практически применимой при анализе результатов исследований из которых является корреляционной.

Нам важно научиться определять параметры уравнений линейной регрессии, используя метод наименьших квадратов.

Понятие корреляции. Корреляционный анализ и его основы. Составление корреляционных таблиц.

Корреляция в математической статистике - вероятностная или статистическая зависимость, не имеющая, вообще говоря, строго функционального характера. В отличие от функциональной, корреляционная зависимость возникает тогда, когда один из признаков зависит не только от данного второго, но и от ряда случайных факторов или же когда среди условий, от которых зависят и тот и другой признаки, имеются общие для них обоих условия.

Пример такого рода зависимости даёт корреляционная таблица. Из таблицы видно, что при увеличении высоты сосен в среднем растет и диаметр их стволов; однако сосны заданной высоты (например, 23 м) имеют распределение диаметров с довольно большим рассеянием. Если в среднем 23-метровые сосны толще 22-метровых, то для отдельных сосен это соотношение может заметным образом нарушаться. Статистическая корреляция в обследованной конечной совокупности наиболее интересна тогда, когда она указывает на существование закономерной связи между изучаемыми явлениями.

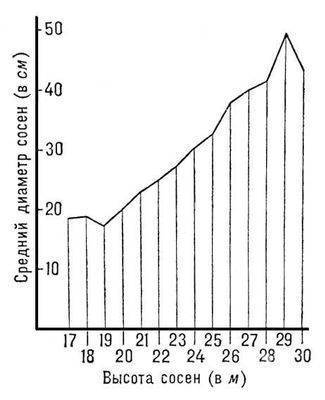
Корреляционный анализ - совокупность основанных на математической теории корреляции методов обнаружения корреляционной зависимости между двумя случайными признаками или факторами.

Корреляционный анализ экспериментальных данных заключает в себе следующие основные практические приёмы:

1) построение корреляционного поля и составление корреляционной таблицы;

2) вычисление выборочных коэффициентов корреляции или корреляционного отношения;

3) проверка статистической гипотезы значимости связи.

Дальнейшее исследование заключается в установлении конкретного вида зависимости между величинами.

Зависимость между тремя и большим числом случайных признаков или факторов изучается методами многомерного корреляционного анализа (вычисление частных и множественных коэффициентов корреляции и корреляционных отношений).

Корреляционное поле и корреляционная таблица являются вспомогательными средствами при анализе выборочных данных. При нанесении на координатную плоскость выборочных точек получают корреляционное поле. По характеру расположения точек поля можно составить предварительное мнение о форме зависимости случайных величин (например, о том, что одна величина в среднем возрастает или убывает при возрастании другой). Для численной обработки результаты обычно группируют и представляют в форме корреляционной таблицы. В каждой клетке корреляционной таблицы приводятся численности гц; тех пар (х, у), компоненты которых попадают в соответствующие интервалы группировки по каждой переменной.

Предполагая длины интервалов группировки (по каждому из переменных) равными между собой, выбирают центры x_i (соответственно y_j) этих интервалов и числа n_ij в качестве основы для расчётов.

Коэффициент корреляции и корреляционное отношение дают более точную информацию о характере и силе связи, чем картина корреляционного поля. Выборочный коэффициента корреляции определяют по формуле:

,

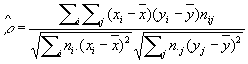где

, ,

, .

При большом числе независимых наблюдений, подчиняющихся одному и тому же распределению, и при надлежащем выборе интервалов группировки коэффициент близок к истинному коэффициенту корреляции r. Поэтому использование как меры связи имеет четко определённый смысл для тех распределений, для которых естественной мерой зависимости служит r (т. е. для нормальных или близких к ним распределений). Во всех др. случаях в качестве характеристики силы связи рекомендуется использовать корреляционное отношение h, интерпретация которого не зависит от вида исследуемой зависимости.

Выборочное значение _y|_x вычисляется по данным корреляционной таблицы:

²_y|_x =

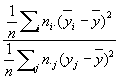
где числитель характеризует рассеяние условных средних значений около безусловного среднего (аналогично определяется выборочное значение _x|_y). Величина _y|_x используется в качестве меры отклонения зависимости от линейной, т. к. обычно ²_y|_x>r², _x|_y>r² и лишь в случае линейной зависимости r²= ²_y|_x= _x|_y. Так, при анализе корреляции между высотой и диаметром северной сосны было обнаружено, что условные средние значения высоты сосны для заданного диаметра связаны нелинейной зависимостью. Корреляционное отношение (высоты к диаметру) в этом случае равно 0,813, а коэффициент корреляции равен 0,762.

Проверка гипотезы значимости связи основывается на знании законов распределения выборочных корреляционных характеристик. В случае нормального распределения величина выборочного коэффициента корреляции считается значимо отличной от нуля, если выполняется неравенство

,

где t_a есть критическое значение t-распределения Стьюдента с (n—2) степенями свободы, соответствующее выбранному уровню значимости a. Если же известно, что r ¹ 0, то необходимо воспользоваться z-преобразованием Фишера (не зависящим от r и n):

.

Исходя из приближённой нормальности z, можно определить доверительные интервалы для истинного коэффициента корреляции r.

В случае, когда изучаются не количественные признаки, а качественные, обычные меры зависимости не годятся. Однако, если удаётся каким-либо образом упорядочить изучаемые объекты в отношении некоторого признака, т. е. прописать им порядковые номера — ранги (по два номера в соответствии с двумя признаками), то в качестве выборочной характеристики связи можно воспользоваться, например, т. н. коэффициентом ранговой корреляции:

,

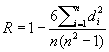где d_i — разность рангов по обоим признакам для каждого объекта. По степени уклонения R от нуля можно сделать некоторое заключение о степени зависимости качественных признаков. Проверка гипотезы независимости признаков при небольшом объёме выборки производится с помощью специальных таблиц, а при n > 10 для вычисления критических значений выборочных коэффициентов пользуются тем, что эти величины распределены приближённо нормально.

Рассмотрим методы составления корреляционных таблиц.

На практике в результате независимых наблюдений над величинами X и Y, как правило, имеют дело не со всей совокупностью всех возможных пар значений этих величин, а лишь с ограниченной выборкой из генеральной совокупности, причем объем n выборочной совокупности определяется как количество имеющихся в выборке пар.

Первоочередной задачей статистической обработки экспериментального материала является систематизация полученных данных и выяснение формы соответствующей генеральной совокупности.

Пусть величина Х в выборке принимает значения x₁, x₂,....x_m, где количество различающихся между собой значений этой величины, причем в общем случае каждое из них в выборке может повторяться. Пусть величина Y в выборке принимает значения y₁, y₂,....y_k, где k - количество различающихся между собой значений этой величины, причем в общем случае каждое из них в выборке также может повторяться. В этом случае данные заносят в таблицу с учетом частот встречаемости. Такую таблицу с группированными данными называют корреляционной.

Первым этапом статистической обработки результатов является составление корреляционной таблицы:

Y\X	x1	x2	...	xm	ny
y1	n12	n21		nm1	ny1
y2		n22		nm2	ny2
...
yk	n1k	n2k		nmk	nyk
nx	nx1	nx2		nxm	n

В первой строке основной части таблицы в порядке возрастания перечисляются все встречающиеся в выборке значения величины X. В первом столбце также в порядке возрастания перечисляются все встречающиеся в выборке значения величины Y. На пересечении соответствующих строк и столбцов указываются частоты n_ij (i=1,2,...,m; j=1,2,...,k) равные количеству появлений пары (x_i;y_i) в выборке. Например, частота n₁₂ представляет собой количество появлений в выборке пары (x₁;y₁). Так же n_xi n_ij, 1≤i≤m, сумма элементов i-го столбца, n_yj n_ij, 1≤j≤k, - сумма элементов j-ой строки и n_xi= n_yj=n

Аналоги формул (3), полученные по данным корреляционной таблицы, имеют вид:

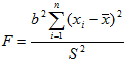(6)