
- •Элементы электрической цепи
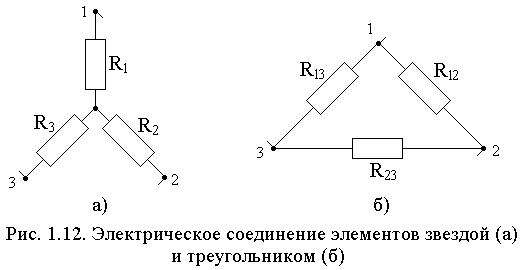
- •Виды соединения электрических элементов
- •Методы расчета линейных электрических цепей
- •Расчет методом эквивалентного преобразования
- •Расчет методом эквивалентного источника напряжения
- •Баланс мощностей. Оценка точности расчёта
- •Применение функции комплексного переменного для представления синусоидальных токов и напряжений. Векторная диаграмма, комплексное сопротивление, треугольник сопротивления
- •Определения
Методы расчета линейных электрических цепей
 Закон
Ома
– падение напряжения на элементе равно
произведению величины сопротивления
этого элемента на величину тока,
протекающего через него.
Закон
Ома
– падение напряжения на элементе равно
произведению величины сопротивления
этого элемента на величину тока,
протекающего через него.
Первый закон Кирхгофа – сумма токов, втекающих в узел, равна сумме токов, вытекающих из узла.
Второй закон Кирхгофа – в замкнутом контуре алгебраическая сумма напряжений источников электрической энергии равна алгебраической сумме падений напряжений на элементах контура. При обходе контура в произвольно выбранном направлении значения напряжений берутся с плюсом, если направление обхода контура и направления напряжений совпадают и берутся с минусом, если этого совпадения нет.
Расчет методом эквивалентного преобразования
Этот метод применяется для не очень сложных пассивных электрических цепей, такие цепи встречаются довольно часто, и поэтому этот метод находит широкое применение. Основная идея метода состоит в том, что электрическая цепь последовательно преобразуется ("сворачивается") до одного эквивалентного элемента, как это показано на рис. 1.13, и определяется входной ток. Затем осуществляется постепенное возвращение к исходной схеме ("разворачивание") с последовательным определением токов и напряжений.
Последовательность расчёта:
1. Расставляются условно–положительные направления токов и напряжений.
2. Поэтапно эквивалентно преобразуются участки цепи. При этом на каждом этапе во вновь полученной после преобразования схеме расставляются токи и напряжения в соответствии с п. 1.
3. В результате эквивалентного преобразования определяется величина эквивалентного сопротивления цепи.
4. Определяется входной ток цепи с помощью закона Ома.
5. Поэтапно возвращаясь к исходной схеме, последовательно находятся все токи и напряжения.
Рассмотрим этот метод на примере (рис. 1.15). В исходной схеме расставляем условно–положительные направления токов в ветвях и напряжений на элементах. Нетрудно согласиться, что под действием источника E с указанной полярностью направление токов и напряжений такое, какое показано стрелками. Для удобства дальнейшего пояснения метода, обозначим на схеме узлы а и б. При обычном расчете это можно не делать.
Далее осуществляем последовательно эквивалентное преобразование схемы. Вначале объединяем параллельно соединенные элементы, и находим (рис. 1.15, б):
![]()
Затем, объединяя все последовательно соединенные элементы, завершаем эквивалентное преобразование схемы (рис. 1.15, в):
![]()
В последней схеме (рис. 1.15, в) находим ток I1:
![]()
Теперь возвращаемся к предыдущей схеме (рис. 1.15, б). Видим, что найдCенный ток I1 протекает через R1, R2,3, R4 и создает на них падение напряжения. Найдем эти напряжения:
![]() .
Возвращаясь
к исходной схеме (рис. 1.15, а), видим,
что найденное напряжение Uаб
прикладывается к элементам R2
и R3.
.
Возвращаясь
к исходной схеме (рис. 1.15, а), видим,
что найденное напряжение Uаб
прикладывается к элементам R2
и R3.
Значит, можем записать, что U2 = U3 = Uа,б
Токи в этих элементах находят из совершенно очевидных соотношений:
Итак, схема рассчитана.
расчет с помощью законов кирхгофа
Этот метод наиболее универсален и применяется для расчета любых цепей. при расчете этим методом первоначально определяются токи в ветвях, а затем напряжения на всех элементах. токи находятся из уравнений, полученных с помощью законов кирхгофа. так как в каждой ветви цепи протекает свой ток, то число исходных уравнений должно равняться числу ветвей цепи. число ветвей принято обозначать через n. часть этих уравнений записываются по первому закону кирхгофа, а часть – по второму закону кирхгофа. все полученные уравнения должны быть независимыми. это значит, чтобы не было таких уравнений, которые могут быть получены путем перестановок членов в уже имеющемся уравнении или путем арифметических действий между исходными уравнениями. при составлении уравнений используются понятия независимых и зависимых узлов и контуров. рассмотрим эти понятия.
независимым узлом называется узел, в который входит хотя бы одна ветвь, не входящая в другие узлы. если число узлов обозначим через к, то число независимых узлов равно (к–1). на схеме (рис. 1.16) из двух узлов только один независим.
независимым контуром называется контур, который отличается от других контуров хотя бы одной ветвью, не входящей в другие контура. в противном случае такой контур называется зависимым.
если число ветвей цепи равно n, то число независимых контуров равно [n – (к–1)].
в схеме (рис. 1.16) всего три контура, но только два независимых контура, а третий – зависим. выделять независимые контура можно произвольно, т. е. в качестве независимых контуров можно выбрать при первом расчете одни, а при втором расчете (повторном) – другие, которые раньше были зависимыми. результаты расчета будут одинаковыми.
если по первому закону кирхгофа составить уравнения для (к–1) независимых узлов, а по второму закону кирхгофа составить уравнения для [n – (к–1)] независимых контуров, то общее число уравнений будет равно:
(K–1) + [n – (K–1)] = n.
Это означает, что для расчёта имеется необходимое число уравнений.
Последовательность расчёта:
1. Расставляем условно – положительные направления токов и напряжений.
2. Определяем число неизвестных токов, которое равно числу ветвей (n).
3. Выбираем независимые узлы и независимые контура.
4 .
С помощью первого закона Кирхгофа
составляем (К–1)
уравнений для независимых узлов.
.
С помощью первого закона Кирхгофа
составляем (К–1)
уравнений для независимых узлов.
5. С помощью второго закона Кирхгофа составляем [n – (К–1)] уравнений для независимых контуров. При этом напряжения на элементах выражаются через токи, протекающие через них.
6. Решаем составленную систему уравнений и определяем токи в ветвях. При получении отрицательных значений для некоторых токов, необходимо их направления в схеме изменить на противоположные, которые и являются истинными.
7. Определяем падения напряжений на всех элементах схемы.
Рассмотрим последовательность расчета на примере схемы, приведенной на рис. 1.16. Учитывая направление источника E, расставляем условно–положительные направления токов и напряжений. В схеме три ветви, поэтому нам необходимо составить три уравнения. В схеме два узла, следовательно, из них только один независимый. В качестве независимого узла выберем узел 1. Для него запишем уравнение по первому закону Кирхгофа:
I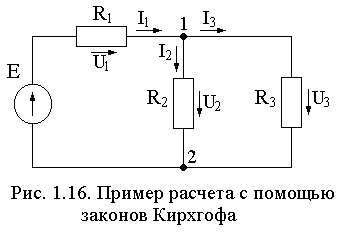 1
= I2
+ I3.
1
= I2
+ I3.
Далее необходимо составить два уравнения по второму закону Кирхгофа. В схеме всего три контура, но независимых только два. В качестве независимых контуров выберем контур из элементов E–R1–R2 и контур из элементов R2– R3. Обходя эти два контура по направлению движения часовой стрелки, записываем следующие два уравнения:
E = I1,R1 + I2R2 ,
0 = – I2R2 + I3R3 .
Решаем полученные три уравнения и определяем токи в ветвях. Затем через найденные токи по закону Ома определяем падения напряжений на всех элементах цепи.
расчет методом контурных токов
Сложные схемы характеризуются наличием значительного числа ветвей. В случае применения предыдущего метода это приводит к необходимости решать систему из значительного числа уравнений.
Метод контурных токов позволяет заметно уменьшить число исходных уравнений. При расчёте методом контурных токов используются понятия независимого контура и зависимого контура, которые нам уже известны. Кроме них в этом методе используются ещё следующие понятия:
– собственный элемент контура – элемент, относящийся только к одному контуру;
– общий элемент контура – элемент, относящийся к двум и более контурам цепи.
Обозначаем, как и раньше, через К число узлов, а через n число ветвей цепи. Тогда число независимых контуров цепи определяется по уже известной формуле [n – (К–1)].
Метод основывается на предположении, что в каждом независимом контуре течёт собственный контурный ток (рис. 1.17), и вначале находят контурные токи в независимых контурах. Токи в ветвях цепи определяют через контурные токи. При этом исходят из того, что в собственных элементах контура токи совпадают с контурным током данного контура, а в общих элементах ток равен алгебраической сумме контурных токов тех контуров, к которым принадлежит данный элемент.
Последовательность расчёта:
1. Определяется число ветвей (n) и число узлов (К) цепи. Находится число независимых контуров [n – (К–1)].
2. Выбирается [n – (К–1)] не зависимых контура.
3. Выбирается условно–положительное направление контурных токов в каждом из независимых контуров (обычно показывается стрелкой).
4. Для каждого из независимых контуров составляется уравнение по второму закону Кирхгофа. При этом падение напряжения на собственных элементах определяется как произведение контурного тока на величину сопротивления, а на общих элементах – как произведение алгебраической суммы всех контурных токов, протекающих через данный элемент, на величину его сопротивления. Обход контура производится, как правило, в направлении собственного контурного тока.
5. Решается система из [n – (К–1)] уравнений и находятся контурные токи.
6. Токи в ветвях схемы находятся следующим образом:
– в собственных элементах контура ток равен контурному току;
– в общих элементах контура ток равен алгебраической сумме токов, протекающих через данный элемент.
Рассмотрим в общем виде применение этого метода для расчёта схемы, приведенной на рис. 1.17.
В этой схеме три ветви и два узла, следовательно, в ней только два независимых контура. Выбираем эти контура и показываем в них направления (произвольно) контурных токов Iк1 и Iк2. Составляем два уравнения по второму закону Кирхгофа:
 .
.
Решив эту систему уравнений, находим контурные токи Iк1 и Iк2. Затем определяем токи в ветвях:
I1 = Iк1 , I3 = Iк2 , I2 = Iк1 – Iк2 .
РАСЧЕТ МЕТОДОМ НАЛОЖЕНИЯ
Метод применяется для расчета цепей, содержащих несколько (два и более) источников электрической энергии. Подчеркнем, что этот метод применим для расчета только линейных цепей. Метод основывается на том положении, что в каждой ветви цепи ток равен алгебраической сумме токов, создаваемых каждым источником. Следовательно, необходимо определить токи, создаваемые каждым источником в отдельности, а затем их просуммировать с учетом направлений.
Последовательность расчета:
1. В электрической цепи оставляют только один источник ЭДС. Вместо исключенного источника ЭДС ставится или резистор, величина которого равна величине внутреннего сопротивления источника ЭДС, или перемычка, если внутреннее сопротивление источника равно нулю.
2. Определяются токи во всех ветвях, создаваемые этим источником ЭДС.
3. Оставляется в цепи следующий источник ЭДС, а с остальными поступают аналогично тому, как сказано в п. 1.
4. Определяются токи в цепи, создаваемые вторым источником ЭДС.
5. Аналогично поступают с оставшимися источниками.
6. Истинные токи в ветвях цепи определяются как алгебраическая сумма токов в этих ветвях, созданных каждым из источников.
Рассчитаем цепь, изображенную на рис. 1.18, методом наложения. Будем считать, что внутренние сопротивления источников ЭДС равны нулю.
В начале оставляем источник E1, а источник E2 убирается и в место него ставится перемычка (рис. 1.18, б). В полученной схеме находим токи методом эквивалентного преобразования:


![]()
![]()
Затем оставляем только источник E2, а вместо E1 ставится перемычка (рис. 1.18, в). В полученной схеме определяем токи в ветвях также методом эквивалентного преобразования:

Находим действительные токи в исходной схеме (рис. 1.18, а) алгебраическим суммированием найденных токов.
Ток I1 равен разности тока I11 и тока I12:
I1 = I11 – I12.
Ток I2 равен сумме токов I21 и I22, т. к. они совпадают по направлению:
I2 = I21 + I22.
Ток I3 равен разности тока I32 и тока I31:
I3 = I32 – I31.
