15.4. Основные геометрические параметры зубчатого колеса цилиндрической передачи

Рассмотрим геометрические параметры зубчатого колеса цилиндрической передачи в плоскости, перпендикулярной оси его вращения (рис. 5.5).

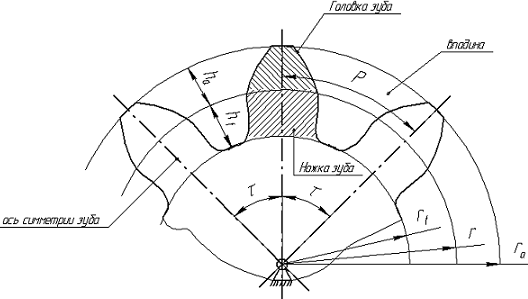
Рис. 10. Геометрические параметры зубчатого колеса

Каждый зуб колеса имеет ось симметрии, проходящую через ось вращения колеса О. Угол между осями симметрии называется угловым шагом τ. Число зубьев колеса z=2π/τ (если τ измеряется в радианах) или z=360º/ τ (если τ измеряется в угловых градусах). Внешняя граница зуба очерчивается окружностью выступов радиусом r_a, а внутренняя часть впадины – окружностью впадин радиусом r_f.

Окружность радиусом r делит зуб по высоте на головку и ножку. Расстояние между одноименными профилями соседних зубьев по дуге этой окружности (или между соседними осями симметрии зубьев) называется окружным шагом P.

Длина окружности диаметром d=2r

L=Pz= πd,

откуда

d=(P/π)×z.

Все остальные геометрические параметры зубчатого колеса в соответствии с ГОСТом пропорциональны модулю m:

высота головки зуба h_a = m;

высота ножки зуба h_f = 1,25 m;

высота зуба h = h_a+h_f = 2,25 m;

радиус окружности выступов

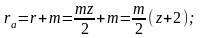
радиус окружности впадин

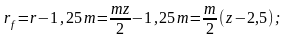
окружной шаг P=π×m;

толщина зуба по делительной окружности

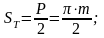
ширина впадин по делительной окружности

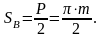
Ширину колеса принимают в пределах в = (10…30)m. Межосевое расстояние двух зацепляющихся колес нулевого зацепления

,

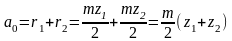где r₁ и r₂ – радиусы делительных окружностей зацепляющих колес; z₁ и z₂ – число их зубьев.

В зацепление друг с другом могут входить только зубчатые колеса, имеющие одинаковый модуль m и окружной шаг P.

Лекция 16

Способы изготовления зубчатых колес. Производящий исходный контур реечного инструмента. Станочное зацепление. Основные расчетные зависимости для определения параметров зубчатого колеса. Планетарные механизмы. Передаточное отношение планетарного механизма.

16.1. Способы изготовления зубчатых колес

Существуют два основных способа изготовления зубчатых колес:

1. копирование: профиль зуба инструмента (протяжка) переносится, и он оставляет след. Способ очень неточный, малопроизводительный и требует наличие инструмента в большом ассортименте, различаемых по модулю и количеству зубьев. Применяется в мелко серийном производстве.

2. огибание: инструменту и заготовке сообщают такое относительное движение, при котором огибающая к положению режущей кромке инструмента очерчивает эвольвенту. Инструмент может быть различным: рейки (гребенки), долбяки и фрезы.

16.2. Производящий исходный контур реечного инструмента

Производящий исходный контур – проекция режущей грани инструмента на плоскость, перпендикулярную оси вращения заготовки (рис. 11).

Рейка – зубчатое колесо с теоретически бесконечно большим количеством зубьев. Как привило, их бывает 8.

r_b  , поэтому все окружности и эвольвента – прямые.

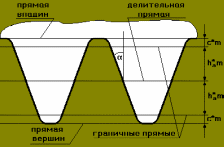
Рис. 11

Все параметры по делительной прямой и по прямым, параллельным делительной прямой, стандартизированы.

=20^о ; h_a* - коэффициент высоты зуба ( h_a*=1).