17. Непрерывные события. Функция распределения.

Рассмотрим случайную величину, изменяющуюся непрерывно. Обозначим её как 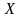. Будем считать, что Х может изменяться от А до В. Тогда вероятность найти Х в диапазоне будет пропорциональна (если охватывается весь диапазон 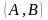, то, очевидно, вероятность должна равняться 1; это опять условие нормировки вероятностей), . Чтобы от пропорции перейти к равенству, надо вставить в правую часть скалярную функцию от аргумента Х: 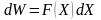. Функция распределения: Функция называется функцией распределения или плотностью вероятности. Для нахождения её явного вида приходится использовать либо экспериментальные данные (феноменологический подход), либо строить некоторое кинетическое уравнение, решением которого служит . В статистической физике кинетическое уравнение получают, исходя из основных законов механики (квантовой статистической механики).

18. Нормировка функции распределения. Вычисление средних статистических величин.

Функция распределения нормируется условием .

Такая нормировка называется нормировкой на единицу. Если в системе имеется 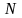одинаковых объектов, справа вместо 1 иногда ставят число . Тогда говорят, что функция распределения нормирована на «число частиц». Правило вычисления средних статистических величин: Вначале записывают тождество , где – та физическая величина, которую надо сопоставлять с экспериментом, или функциональные зависимости которой от разных параметров надо исследовать. Тождество интегрируют с функцией распределения (оно остается тождеством): . Интегрирование проводится по всем допустимым значениям Х. Затем предполагается, что в первом интеграле стоит не сам оператор , а его среднее статистическое значение , которое является независящей от Х константой. Константу вынести из под интеграла, . Поскольку функция распределения предполагается нормированной на единицу, стоящий слева интеграл равен 1 и мы получает формулу для расчета среднего .

19. Распределение Максвелла для одномерного движения частиц. Интеграл Френеля. Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию.

Интегралы Френеля S(x) и C(x) — это специальные функции, названные в честь Огюстена Жана Френеля и используемые в оптике. Они возникают при расчёте дифракции Френеля и определяются как

20. Распределение Максвелла по скоростям. Нормировка.

Первым распределением статистической физики было распределение частиц идеального газа. находящегося в равновесии, по скоростям. Оно было получено Максвеллом с помощью теории вероятностей и кинетических представлений. Максвелл нашел число частиц ансамбля, скорости которых лежат в интервале . Это число можно записать в виде , где функция скорости называется функцией распределения Максвелла по скоростям.

Нормировка - это корректировка ряда (вектора) значений (обычно представляющих набор измерений, например, переменная, хранящая рост людей, выраженный в дюймах) в соответствии с некоторыми функциями преобразования, с целью сделать их более удобными для сравнения. Например, разделив эти значения на 2.54, мы получим измерения роста в метрической системе.