7. Внутренняя энергия для многоатомных частиц. Теплоемкость при постоянном объеме. , . Обратим внимание на то, что в числителе последних формул стоит число 3. Это следствие того, что материальная точка (атом) имеет три степени свободы (по числу координат ). В случае молекул, состоящих из n атомов, это число надо заменить на число степеней свободы отдельной молекулы. Оно подсчитывается по формуле , где s – число наложенных на молекулe связей (например, в молекуле имеется только одна связь, в молекуле две связи и т.п.). Соответственно, полная внутренняя энергия сложных молекул будет равна . В первое начало войдет производная по температуре и начало примет общий вид: . Теплоемкость при постоянном объеме. На этом этапе изучения первого начала термодинамики обычно вводят понятие теплоемкости при постоянном объеме : , так что . Заметим, что при рассмотрении одного моля веществ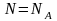а , а , что позволяет записать полученные формулы, используя найденную экспериментально универсальную газовую постоянную R.

8. Тепловые машины: замкнутый и незамкнутый циклы.

Тепловой машиной называется любое устройство, преобразующее внутреннюю энергию в механическую. Такие машины могут быть «одноразовыми» и «циклическими». К одноразовым можно отнести, например, ружьё: заряд пороха, сгорая, создает некоторое количество горячих газов, которые расширяются и выталкивают снаряд, совершая механическую работу. Однако коэффициент полезного действия «одноразовых» устройств обычно невелик, а действие кратковременно.

Более эффективны циклические тепловые машины. Это паровая машина паровоза, бензиновый двигатель внутреннего сгорания, турбинные двигатели авиационных двигателей и другие подобные устройства. Теоретическое описание циклических тепловых машин проводилось разными авторами. Так, известен цикл Дизеля, цикл Отто (цикл бензинового двигателя), цикл Карно. Наиболее важным считается цикл Карно.

9. Цикл Карно.

Цикл Карно на диаграмме (P0V) состоит из 4 участков. Первый и третий это изотермические процессы, проходящие при постоянных температурах 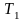и – два адиабатных процесса (система не обменивается теплом с окружающей средой). 10. Идеальная тепловая машина Карно, её КПД. Как и большинство циклически действующих тепловых машин, машина Карно состоит из нагревателя, рабочего тела, потока механической работы и холодильника. Различия связаны с используемыми в цикле изопроцессами (другие диаграммы типа (POV)). Стрелка из нагревателя показывает на передачу тепла рабочему телу. Стрелка 3 показывает, что машина Карно совершает полезную работу А. Стрелка, входящая в холодильник показывает на передачу тепла , от рабочего тела холодильнику. КПД определяется стандартным образом, то есть как отношение полезной работы к затраченной работе. В нашем случае,

.

10. Идеальная тепловая машина Карно, ее кпд.

Всегда количество тепла , то есть КПД машины всегда меньше единицы. Однако главная ценность машины Карно заключается в связанной с машиной теоремой Карно.

Теорема Карно утверждает, что КПД идеальной тепловой машины не зависит от природы рабочего тела, количеств тепла или , а зависит только от температур нагревателя и холодильника, . Следствием теоремы Карно является утверждение, что любая тепловая машина не может иметь КПД, больший (или даже равный), чем КПД идеальной машины Карно. Заметим, что в действительности даже сама машина Карно должно иметь еще меньший КПД, поскольку никакие потери энергии на преодоление сил трения не учитывались.

11. Обратимые и необратимые термодинамические процессы.

Пусть имеется замкнутый цикл переходов между термодинамическими состояниями типа 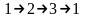. Назовем его «прямым» замкнутым циклом. Цикл называется «обратным». Если можно переводить систему и прямым образом, и обратным, то говорят, что в такой системе существуют обратимые процессы. В противном случае процесс необратимый. Обратимость процессов связана с понятием энтропии (см. определение ниже). В этом случае Второе начало утверждает, что энтропия замкнутой системы не убывает (остается постоянной у обратимых процессов и возрастает у остальных процессов). Сразу заметим, что у подсистемы, т.е. у части замкнутой системы энтропия может убывать с одновременным ростом энтропии всей системы.