4. Модель газа Ван-дер-Ваальса.

В отличие от идеального газа, модель Ван-дер-Ваальса лучше соответствует реальным газам. Она учитывает рассеяние частиц друг на друге (то есть молекулярные силы) или внутреннее давление , а также собственный объем моля частиц . Внутреннее давление можно выразить формулой , где – константа для данного газа. Если газ содержит молей, то уравнение состояния Ван-дер-Ваальса имеет вид: . Поправки к уравнению идеального газа должны быть много меньше параметров . Указанные примеры относятся к однородным системам, в которых нет переноса массы, импульса и энергии (отсутствие потоков массы, импульса и энергии является условием термодинамического равновесия). Термодинамическое равновесие – очень интересное состояние системы. Не надо думать, что там нет потоков энергии, импульса и вещества. Потоки есть, но они одинаковы по всем направлениям, то есть компенсируют друга. Это динамическое равновесие.

5. Гипотеза о молекулярном хаосе. Средняя энергия частиц ансамбля. Модуль средней скорости.

Средняя энергия частиц ансамбля. Модуль средней скорости. Возникновение динамического равновесия является следствием очень давней гипотезы о молекулярном хаосе, согласно которой все направления в пространстве равноправны для термодинамической системы (система изотропна). Отталкиваясь от идеи молекулярного хаоса после небольших преобразований можно получить важное соотношение, связывающее температуру ансамбля со средней энергией, приходящейся на одну частицу (атом или материальную точку; для молекул картина несколько сложнее): . Указанное равенство считается определением термодинамической или абсолютной температуры. Из него следует возможность определения средней скорости частиц: , . Вектор средней скорости, по гипотезе о молекулярном хаосе, равен нулю. В статистической физике средние значения энергии и скорости получают без гипотезы о молекулярном хаосе на основе статистических распределений. Если термодинамическое равновесие нарушено и в ансамбле возникли потоки, то говорят, что возникают процессы переноса вещества (диффузия), энергии (теплоперенос, теплопроводность), импульса (внутреннее трение или вязкость). Возможны и другие процессы переноса, в частности, возникновение электрического тока.

6. Первое начало термодинамики.

Термодинамика построена на базе нескольких постулатов, которые называются началами. Первое начало – это закон сохранения энергии, учитывающий передачу системе энергии в виде тепла или , изменение внутренней энергии – кинетической энергии скрытого движения частиц ансамбля , и совершаемой системой работы : , или, что точнее, . Этим формам часто придают несколько иной вид. Учтем, что . Тогда первое начало можно записать как . Если система представляет собой идеальный одноатомный газ и средняя энергия одной частицы равна , то полная внутренняя энергия равна 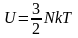. 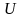Изменение внутренней энергии можно получить, продифференцировав по температуре (число частиц считается постоянным): , .
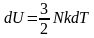