Часть I. Механика.

1. Механическое движение.

Механическое движение - изменение положения тела в пространстве с течением времени. Для математического описания такого движения надо ввести понятие системы отсчета. Так как экспериментально было установлено, что геометрическое пространство трехмерно, то для введения системы отсчета надо указать четыре точки, не лежащие на одной прямой или в одной плоскости. Одну из них принимают за начало отсчета, остальные указывают направление трех координатных осей. Если оси ортогональны (перпендикулярны), то система отсчета называется Декартовой. Если же углы между осями отличаются от прямых, то систему называют косоугольной.

2. Система отсчета. Система координат. Радиус вектор. Орты.

Положительные направления осей указываются ортами или единичными векторами. В Декартовых системах координат обычно используют три орта. Тогда положение данной точки пространства однозначно указывается радиус-вектором, например , где 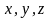– проекции координат точки на соответствующие оси. Если точка движется, то радиус-вектор становится функцией времени.

3. Система СИ. Основные механические единицы.

В настоящее время принято использовать Международную систему единиц (СИ). В этой системе основными механическими единицами считаются метр (м), килограмм (кг), секунда (с). С их помощью вводят «производные» величины.

4. Материальная точка.

Материальной точкой называется объект малых размеров, форма которого не влияет на характер движения.

5. Средняя и мгновенная скорости.

Средняя скорость – грубая характеристика движения. Она становится точнее, если уменьшать . Если рассматривать предел отношения при , то есть заменить отношение производной, то можно ввести мгновенную скорость в момент времени t.

6. Среднее и мгновенное ускорения.

Аналогичным образом вводят среднее и мгновенное ускорения. Ускорение – это скорость изменения скорости, то есть мгновенное ускорение определяется первой производной (по времени) скорости, или, что то же самое, второй производной радиус-вектора: (м/с²).

7. Импульс и сила.

Импульсом материальной точки называют векторную величину, полученную при перемножении массы точки на её мгновенную скорость: 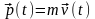Сила – векторная величина. Ее обычно обозначают как . В классической механике силу связывают с изменением импульса: .

8. Кинетическая, потенциальная, полная механическая энергии.

Кинетическая энергия – энергия механической системы, зависящая от скоростей движения ее точек. По определению, кинетическая энергия материальной точки равна: . Потенциальная энергия – скалярная физическая величина, характеризующая способность некого тела (материальной точки) совершать работу за счет своего нахождения в поле действия сил. Полная механическая энергия – сумма потенциальной и кинетической энергий тела.

9. Состояние механической системы.

Состояние механической системы. Механическая система обладает определённым числом степеней свободы, а её состояние описывается с помощью обобщённых координат и соответствующих им обобщённых импульсов.

10. Число степеней свободы.

Степени свободы – совокупность независимых координат перемещения и (или) вращения, полностью определяющая положение системы или тела.

11. Основная задача механики.

Основная задача механики – определять положение (координаты) движущегося тела в любой момент времени.

12. Закон всемирного тяготения.

, где – постоянная Всемирного тяготения, и – взаимодействующие массы, расстояние между которыми равно , дробь – орт, указывающий направление действия силы и проведенный из первой массы, знак минус показывает, что при взаимодействии масс возникает сила притяжения.

13. Физический смысл Первого закона Ньютона.

Первый закон – закон инерции. Как и остальные законы Ньютона, он является результатом обобщения экспериментальных данных. Закон утверждает следующее. Если результирующая всех сил, действующих на материальную точку, равна нулю, то материальная точка находится в состоянии покоя или равномерного прямолинейного движения. Первый закон исправляет ошибку Аристотеля. Он утверждает, что в природе существуют инерциальные системы отсчета, относительно которых материальная точка может покоиться.