Модифицированный метод Эйлера
Известно несколько модифицированных методов Эйлера. Здесь будет использоваться та модификация, в которой производная определяется в середине каждого шага интегрирования, или, если вычисления выполняются только в узловых точках, то
.
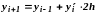Этот метод фактически не относится к одношаговым. Для начала расчета необходимо выполнить вычисления в одном предыдущем шаге. И шаг интегрирования здесь уже нельзя изменять. Он является более точным, чем обычный метод Эйлера. Абсолютно точным он является для функций второго порядка.
Значение при t=13c переписываем из распечаток, при t=13.5 c с метода Эйлера.
Таблица 4.9. – Модифицированный метод Эйлера
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
t,s |
V,m/s |
X,m |
H,m |
Xc,m |
Rc,m |
β° |
q° |
e° |
13 |
460 |
2859 |
149 |
|
|
|
-0,9 |
|
13,5 |
474 |
3093 |
145 |
7600 |
4507,225 |
-0,57205 |
-1 |
0,427951 |
14 |
487,9219 |
3332,928 |
140,7276 |
7400 |
4067,276 |
-0,57374 |
-0,93527 |
0,361531 |
14,5 |
501,0434 |
3580,857 |
137,0357 |
|
|
|
-1,03468 |
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
cos(q) |
sin(q) |
V*cos(q) |
V*sin(q) |
m,kg |
P(H) |
a(H) |
g(H) |
mg |
0,999848 |
-0,01745 |
473,9278 |
-8,27244 |
31,025 |
99600 |
339,737 |
9,806 |
304,2312 |
0,999867 |
-0,01632 |
487,8569 |
-7,96426 |
30,6 |
99640 |
339,753 |
9,806 |
300,0636 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
M |
qS |
Cxtr |
Cxд |
Cxво |
Cx0 |
Cyalp |
Alp1 |
Cx1 |
1,395197 |
10721,5 |
0,029 |
0 |
0,048325 |
0,077325 |
3,28 |
0,457817 |
0,000927 |
1,436108 |
11364,04 |
0,029 |
0 |
0,047334 |
0,076334 |
3,314 |
0,422871 |
0,000898 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
Cxa |
Xa |
Nxa |
Vdot |
DCY/AR |
Cya |
Ya |
Nya |
TetaDot |
0,078252 |
838,9786 |
2,829977 |
27,92189 |
0,006704 |
0,02626 |
281,5486 |
0,970092 |
-0,03527 |
0,077232 |
877,6632 |
2,740387 |
27,04338 |
0,006059 |
0,024502 |
278,4402 |
0,969751 |
-0,0347 |
Для заданного значения Н, параметры атмосферы , а также величины меняются не значительно, поэтому их изменениями можно пренебречь.
Таблица 4.13. – Определение угла атаки при t=14с
Teta(dot) |
-0,0097 |
|
|
Nya |
0,965151 |
|
|
А |
295,1042 |
|
|
АВ |
0,027525 |
|
|
Ср |
0,15856 |
Dcy(Alp0) |
DCY/AR1 |
Cya(alp) |
3,28 |
0 |
0,006134 |
Alp1 |
Alp2 |
|
|
0,008005 |
0,00799 |
радианы |
|
0,458634 |
0,457817 |
градусы |
|
Таблица 4.14. – Определение угла атаки при t=14.5с
Teta(dot) |
-0,0012 |
|
|
Nya |
0,9650119 |
|
|
А |
291,0617 |
|
|
АВ |
0,025613 |
|
|
Ср |
0,149595 |
Dcy(Alp0) |
DCY/AR1 |
Cya(alp) |
3,314 |
0 |
0,006704 |
Alp1 |
Alp2 |
|
|
0,007395 |
0,00738 |
радианы |
|
0,42369 |
0,422871 |
градусы |
|
При применении модифицированного метода Эйлера:
