Вопрос 32.Макроскопческие процессы(хаотические и упорядоченные).Термодинамические процессы(обратимые и необратимые).

Порядок и беспорядок в природе. Макроскопические процессы

1)Хаотические макроскопические процессы-процессы, приводящие к хаотическому(беспорядоченному) размещению объектов.

Особенности хаотических макр. процессов:

1)Для их описания используются статистические представления

2)Хаотические макр. процессы имеют направленность к наиболее вероятному состоянию.

3)Возврат в предшествующие состояния, для большинства систем, практически нереализуем.

2)Упорядоченные макроскопические процессы-процессы, приводящие к строго структурированному, взаимообусловленному размещению объектов.

Биологические процессы- по своей сути упорядоченные процессы.

Термодинамические процессы

1)Обратимые термодинамические процессы- идеальный процесс в термодинамической системе, допускающий возврат системы в исходное состояние, с воспроизведением состояний, в которых была система.

Особенности обратимых термодинамических процессов:

1)Эти процессы присущи консервативным системам

2)Эти процессы являются квази-статическими (близровновесными): они выражают равновесные переходы системы, из одного состояния, в другие.

2)Необратимые хаотические процессы-реальный, самопроизвольный процесс термодинамической системы.

Для описания степени беспорядка в системе используется понятие ЭНТРОПИИ.

Вопрос 33. Энтропия, ее свойства. Расчет изменения энтропии у идеального газа.

Энтропия(S)-функция состояния системы, которая выражает степень беспорядка в ней.

При возврате системы в исходное состояние: ∆S=0

Энтропию можно выразить несколькими способами:

1)По Больцману

k-постоянная Больцмана.

W-термодинамическая вероятность реализации состояния системы.

Е

I

II

W⁽¹⁾

W= W⁽¹⁾*W⁽²⁾

W⁽²⁾

сли система состоит из двух независимых систем

S=S⁽¹⁾+S⁽²⁾

Энтропия системы- сумма отдельных независимых подсистем.

2)По Клазиусу(расчет энтропии у ИДЕАЛЬНОГО газа)

,

где —приращение энтропии;

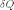—минимальная теплота, подведенная к системе;

T — абсолютная температура процесса;

Это уравнение применимо к любому уравнению идеального газа.

Свойства энтропий:

1) энтропия – величина аддитивная, т.е. энтропия системы равна сумме энтропий отдельных элементов.

2) если в изолированной системе происходит обратимые процессы, то её энтропия остаётся неизменной.

3) если в изолированной системе происходит необратимые процессы, то её энтропия возрастает.

4) энтропия изолированной системы не может уменьшаться.

Возрастать энтропия может по двум причинам:

1)вследствие необратимого процесса перехода системы в равновесное (более вероятное) состояние;

2)вследствие сообщения системе определенного количества теплоты.

Вопрос 34.Второе начало термодинамики(формулировки) и его смысл.

Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.

Существуют несколько эквивалентных формулировок второго начала термодинамики:

1 )по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу; 2) по Клаузиусу: невозможен круговой процесс, единственным результатом которо­го является передача теплоты от менее нагретого тела к более нагретому.

/* Эквивалентность этих формулировок легко показать. В самом деле, допустим, что постулат Клаузиуса неверен, то есть существует процесс, единственным результатом которого была бы передача тепла от более холодного тела к более горячему. Тогда возьмем два тела с различной температурой (нагреватель и холодильник) и проведем несколько циклов тепловой машины, забрав тепло   у нагревателя, отдав   холодильнику и совершив при этом работу 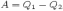 . После этого воспользуемся процессом Клаузиуса и вернем тепло   от холодильника нагревателю. В результате получается, что мы совершили работу только за счет отъёма теплоты от нагревателя, то есть постулат Томсона тоже неверен.

С другой стороны, предположим, что неверен постулат Томсона. Тогда можно отнять часть тепла у более холодного тела и превратить в механическую работу. Эту работу можно превратить в тепло, например, с помощью трения, нагрев более горячее тело. Значит, из неверности постулата Томсона следует неверность постулата Клаузиуса.

Таким образом, постулаты Клаузиуса и Томсона эквивалентны. */

Другая формулировка второго начала термодинамики основывается на понятии энтропии:

Второе начало термодинамики можно сформулировать как закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает.

/* Здесь существенно, что речь идет о замкнутых системах, так как в незамкнутых системах энтропия может вести себя любым образом (убывать, возрастать, оставаться постоянной). Кроме того, отметим еще раз, что энтропия остается постоянной в замкнутой системе только при обратимых процессах. При необратимых процессах в замкнутой системе энтропия всегда возрастает. */

S

, где k – постоянная Больцмана, W – термодинамическая вероятность, реализующая состояние системы. Формула Больцмана, которая определяет количественную связь между энтропией S и термодинамической вероятностью W.

Smax

t

Учитывая то, что в системе возможно локальное понижение энтропии с опорой на молекулярно-статистические представления, формулировка второго начала термодинамики принимает уточненный вид:

S

В замкнутой и адиобатически изолированной системе наиболее вероятным возможен процесс, сопровождающийся возрастанием энтропии.

Флуктация(отклонения)

t