47) Законы сохранения при упругоми неупругом взаимодействиях.

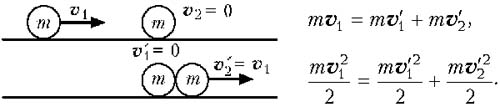
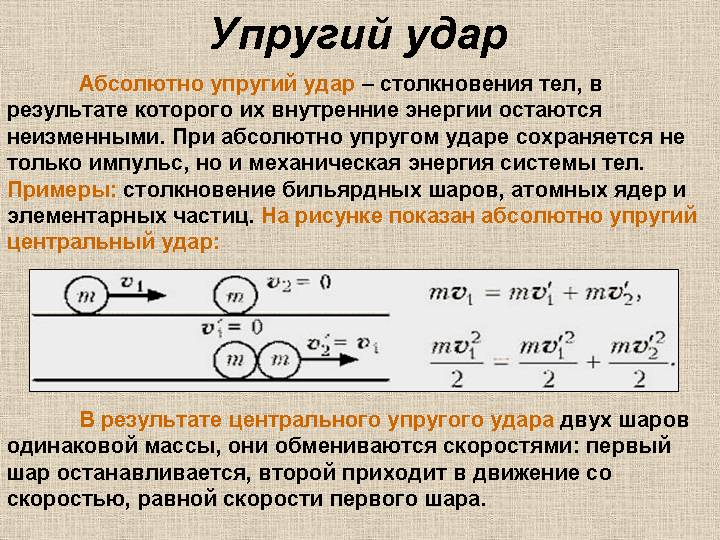
В результате центрального упругого удара двух шаров одинаковой массы, они обмениваются скоростями: первый шар останавливается, второй приходит в движение со скоростью, равной скорости первого шара.

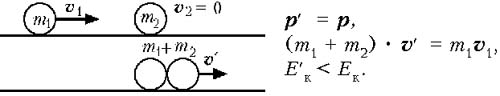
После неупругого соударения два шара движутся как одно целое со скоростью, меньшей скорости первого шара до соударения.

48) 49) В инерциальной системе отсчета ускорение материальной точки пропорционально силе, приложенной к ней:

ma = F

50) Уравнение движения в неинерциальных системах отсчета. Основное уравнение динамики относительного движения материальной точки имеет вид:

,

где   — масса тела,   — ускорение тела относительно неинерциальной системы отсчёта,   — сумма всех внешних сил, действующих на тело,   — переносное ускорение тела,   — кориолисово ускорение тела.Это уравнение может быть записано в привычной форме Второго закона Ньютона, если ввести фиктивные силы инерции:  — переносная сила инерции  — сила Кориолиса

51) Силы инерции— силы, обусловленные ускоренным движением неинерциальной системы отсчета (НСО) относительно инерциальной системы отсчета (ИСО). Основной закон динамики для неинерциальных систем отсчета:  , где   — сила, действующая на тело со стороны других тел;

  — сила инерции, действующая на тело относительно поступательно движущейся НСО.   — ускорение НСО относительно ИСО. Она появляется, например, в самолете при разгоне на взлетной полосе;

  — центробежная сила инерции, действующая на тело относительно вращающейся НСО.   — угловая скорость НСО относительно ИСО,   — расстояние от тела до центра вращения;

  — кориолисова сила инерции, действующая на тело, движущееся со скоростью   относительно вращающейся НСО.    — угловая скорость НСО относительно ИСО (вектор направлен вдоль оси вращения в соответствии с правилом правого винта).

52)Центробежная сила:  F = mv²/r подставим =>   F = ma = mv²/r.

53) Момент импульса частицы- L=r*p момент импульса — это векторное произведение радиус-вектора на импульс.

54)Момент силы частицы - - где   — сила, действующая на частицу, а   — радиус-вектор частицы.

Момент силы относительно оси - m_z(F)=пр_zm_A(F) Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.

55) Момент импульса

56) Уравнение моментов -

57)  Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точкине изменяется с течением времени. 

   Поэтому  , то есть или . Это один из фундаментальных законов природы. Аналогично для замкнутой системы тел, вращающихся вокруг оси z: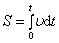          отсюда                   или          .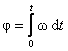

58)Вращение твердого тела: нужно пользоваться угловой скоростью:

Если нас интересует линейная скорость движения какой-то точки тела, расположенной на расстоянии r от оси вращения, то ее можно вычислить по известной нам формуле

59)   Основной закон динамики вращательного движения твердого тела , где F – сила, приложенная к телу массой m; а – линейное ускорение тела.

60) Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что  , получим .

Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса):  .

Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело: .

Момент инерции

61)

62) Вычисление моментов инерции тел правильной формы: стержня:

Цилиндра: сферы: шара: плоских фигур

63) Теоре́ма Гю́йгенса — Ште́йнера - где  — известный момент инерции относительно оси, проходящей через центр масс тела,

 — искомый момент инерции относительно параллельной оси,

 — масса тела,

 — расстояние между указанными осями.

64) Свободные оси. Гироскопы. Для того чтобы сохранить положение оси вращения твердого тела с течением времени неизменным, используют подшипники, в которых она удерживается. Но существуют такие оси вращения тел, которые не изменяют своей ориентации в пространстве без действия на нее внешних сил. Эти оси называются свободными осями (или осями свободного вращения). Можно показать, что в любом теле существуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями – они называются главными осями инерции тела.

Например, главные оси инерции однородного прямоугольного параллелепипеда проходят через центры противоположных граней; главными осями инерции шара являются любые три взаимно перпендикулярные оси, проходящие через центр масс.

Свойство свободных осей сохранять свое положение в пространстве широко применяется в технике. Наиболее интересны в этом отношении гироскопы – массивные однородные тела, вращающиеся с большой угловой скоростью около своей оси симметрии, являющейся свободной осью. Гироскопы применяют в различных гироскопических навигационных приборах (гирокомпас, гирогоризонт и т.д.), а также в различных автопилотах.

65) Главные моменты инерции:

66) Момент инерции относительно произвольной оси

Момент инерции

67) Гироско́п — устройство, способное реагировать на изменение углов ориентации тела, на котором оно установлено, относительно инерциальной системы отсчета. Простейший пример гироскопа — юла.

68) Прецессия — явление, при котором момент импульса тела меняет своё направление в пространстве под действием момента внешней силы. Наблюдать прецессию достаточно просто. Нужно запустить волчок и подождать, пока он начнёт замедляться. Первоначально ось вращения волчка вертикальна. Затем его верхняя точка постепенно опускается и движется по расходящейся спирали. Это и есть прецессия оси волчка.

Главное свойство прецессии — безынерционность: как только сила, вызывающая прецессию волчка, пропадёт, прецессия прекратится, а волчок займёт неподвижное положение в пространстве. В примере с волчком этого не произойдет, поскольку в нём вызывающая прецессию сила — гравитацияЗемли — действует постоянно.

Можно получить эффект прецессии, не дожидаясь замедления вращения волчка: толкните его ось (приложите силу) — начнётся прецессия. С прецессией напрямую связан другой эффект, показанный на иллюстрации ниже — это нутация — колебательные движения оси прецессирующего тела. Скорость прецессии и амплитуда нутации связаны со скоростью вращения тела (изменяя параметры прецессии и нутации в случае, если есть возможность приложить силу к оси вращающегося тела, можно изменить скорость его вращения).

69) Кинетическая энергия системы есть энергия движения центра масс плюс энергия движения относительно центра масс:

,

где   — полная кинетическая энергия,   — энергия движения центра масс,   — относительная кинетическая энергия.

Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы в поступательном движении и энергии системы во вращательном движении относительно центра масс.