
Формулы, выводы.
Система отсчета: например в декартовых системах:
 ,
, 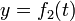 ,
, 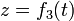
это совокупность тела отсчета, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел.
2)
Радиус-вектора:
Декартовы:
![]() Полярные, цилиндрические и сферические:
Полярные, цилиндрические и сферические:
![]()
3![]()
 )
а)Перемещение
при равномерном
движении:
)
а)Перемещение
при равномерном
движении:
б)Перемещение
при равноускоренном движении:
Для
вычисления перемещения: 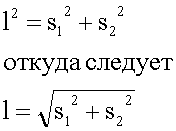
4
)Путь-длина траектории. Для
вычисления полного пути: ![]()
5) Средняя скорость:v=at/2, v=v-vo/2 6 )Мгновенная скорость: а)В векторном виде: V=Vo+at, где V, Vo, a - векторы б)В скалярном:V=Vo+at, где V, Vo, a - проекции векторов на выбраную ось. в) формула для проекций: S=(Vx^2-Vox^2)/2a
7)
Среднее
ускорение>
– это отношение изменения скорости к
промежутку времени, за который это
изменении произошло. Определить среднее
ускорение можно формулой:![]()
Мгновенное
ускорение тела
![]()
8)
Средняя путевая скорость
![]()
9)Траектория движения: F=dp/dt, p=m*v, F=m*g+Fсопр +Fархимеда
10)Нахождение
радиус-вектора и скорости с известным
ускорением:
![]()
11)
Величину тангенциального ускорения -
в смысле проекции вектора ускорения на
единичный касательный вектор траектории
- можно выразить так:
![]() где
где ![]() -
путевая скорость вдоль траектории,
совпадающая с абсолютной величиной
мгновенной скорости в данный момент.
Если использовать для единичного
касательного вектора обозначение
-
путевая скорость вдоль траектории,
совпадающая с абсолютной величиной
мгновенной скорости в данный момент.
Если использовать для единичного
касательного вектора обозначение ![]() ,
то можно записать тангенциальное
ускорение в векторном виде:
,
то можно записать тангенциальное
ускорение в векторном виде:
![]()
Вывод:
![]()
12)
Нормальное
ускорение: ![]()
13) Теорема вращения Эйлера утверждает, что любое вращение трёхмерного пространства имеет ось.Таким образом, вращение может быть описано тремя координатами: двумя координатами оси вращения (например,широта и долгота) и углом поворота.Для заданного единичного вектора n и угла φ обозначим R(φ, n) вращение в направлении вектора n против часовой стрелки на угол φ. Тогда:
R(0, n) — тождественное отображение для любого n
R(φ, n) = R(−φ, −n)
R(π + φ, n) = R(π − φ, −n)
Для любого вращения существует единственный угол φ, для которого 0 ≤ φ ≤ π, при этом:
n определяется однозначно, если 0 < φ < π
n любое, если φ = 0
n определяется однозначно с точностью до знака, если φ = π (то есть, вращения R(π, ±n) одинаковы).
14)
Углова́я
ско́рость — векторная физическая
величина, характеризующая скорость
вращения тела. Вектор угловой скорости
по величине равен углу поворота
тела в единицу времени:
![]()
15)Угловое
ускорение:
![]()
16) Скорость точки при вращении: Скорость точки V=dS/dt=dφ⋅R/dt=ωR
Скорость
направлена по касательной к траектории,
поэтому можно написать![]()
17) Сложение поступательного и вращательного движений

18) Разложение движения на поступательное и вращательное. Плоскопараллельным (или плоским) называется такое движение твердого тела, при, котором все его точки перемещаются параллельно некоторой фиксированной плоскости П (рис. 28). Плоское движение совершают многие части механизмов и машин, например катящееся колесо на прямолинейном участке пути, шатун в кривошипно-ползунном механизме и др. Частным случаем плоскопараллельного движения является вращательное движение твердого тела вокруг неподвижной оси.
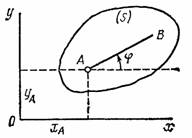
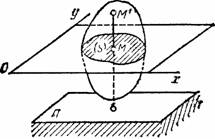
Рис.28 Рис.29
Рассмотрим сечение S тела какой-нибудь плоскости Оxy, параллельной плоскости П (рис.29). При плоскопараллельном движении все точки тела, лежащие на прямой ММ’, перпендикулярной течению S, т. е. плоскости П, движутся тождественно.
Отсюда заключаем, что для изучения движения всего тела достаточно изучить, как движется в плоскости Оху сечение S этого тела или некоторая плоская фигура S. Поэтому в дальнейшем вместо плоского движения тела будем рассматривать движение плоской фигуры S в ее плоскости, т.е. в плоскости Оху.
Положение
фигуры S в
плоскости Оху определяется
положением какого-нибудь проведенного
на этой фигуре отрезка АВ (рис.
28). В свою очередь положение отрезка АВ можно
определить, зная координаты ![]() и
и ![]() точки А и
угол
точки А и
угол ![]() ,
который отрезок АВ образует
с осью х.
Точку А,
выбранную для определения положения
фигуры S,
будем в дальнейшем называть полюсом.
,
который отрезок АВ образует
с осью х.
Точку А,
выбранную для определения положения
фигуры S,
будем в дальнейшем называть полюсом.
При движении фигуры величины и и будут изменяться. Чтобы знать закон движения, т. е. положение фигуры в плоскости Охув любой момент времени, надо знать зависимости
![]() .
.
Уравнения, определяющие закон происходящего движения, называются уравнениями движения плоской фигуры в ее плоскости. Они же являются уравнениями плоскопараллельного движения твердого тела.
Первые
два из уравнений движения определяют
то движение, которое фигура совершала
бы при
=const;
это, очевидно, будет поступательное
движение, при котором все точки фигуры
движутся так же, как полюс А. Третье
уравнение определяет движение,
которое фигура совершала бы при ![]() и
и ![]() ,
т.е. когда полюс А неподвижен;
это будет вращение фигуры вокруг
полюса А.
Отсюда можно заключить, что в общем
случае движение плоской фигуры в ее
плоскости может рассматриваться как
слагающееся из поступательного
движения, при котором все точки фигуры
движутся так же, как полюс А,
и из вращательного движения вокруг
этого полюса.
,
т.е. когда полюс А неподвижен;
это будет вращение фигуры вокруг
полюса А.
Отсюда можно заключить, что в общем
случае движение плоской фигуры в ее
плоскости может рассматриваться как
слагающееся из поступательного
движения, при котором все точки фигуры
движутся так же, как полюс А,
и из вращательного движения вокруг
этого полюса.
Основными
кинематическими характеристиками
рассматриваемого движения являются
скорость и ускорение поступательного
движения, равные скорости и ускорению
полюса ![]() ,
, ![]() ,
а также угловая скорость
,
а также угловая скорость ![]() и
угловое ускорение
и
угловое ускорение ![]() вращательного
движения вокруг полюса.
вращательного
движения вокруг полюса.
19) МГНОВЕННАЯ ОСЬ ВРАЩЕНИЯ. прямая, неподвижная в данный момент в нек-рой инерциальной системе отсчёта, относительно к-рой сложное движение твёрдого тела в этот момент можно представить как вращат. вокруг этой прямой. М. о. в. может лежать как внутри тела, так и вне его. С течением времени положение М. о. в. изменяется относительно как неподвижной системы отсчёта, так и системы отсчёта, движущейся вместе с телом.
20) Материа́льная то́чка (частица) — простейшая физическая модель в механике — идеальное тело, размеры которого равны нулю, можно также считать размеры тела бесконечно малыми по сравнению с другими размерами или расстояниями в пределах допущений исследуемой задачи. Положение материальной точки в пространстве определяется как положение.
Практически под материальной точкой понимают обладающее массой тело, размерами и формой которого можно пренебречь при решении данной задачи
21)Масса – мера инертности тела. Пассивная гравитационная масса показывает, с какой силой тело взаимодействует с внешними гравитационными полями — фактически эта масса положена в основу измерения массы взвешиванием в современнойметрологии.
Активная гравитационная масса показывает, какое гравитационное поле создаёт само это тело — гравитационные массы фигурируют в законе всемирного тяготения.
Инертная масса характеризует инертность тел и фигурирует в одной из формулировок второго закона Ньютона. Если произвольная сила винерциальной системе отсчёта одинаково ускоряет разные исходно неподвижные тела, этим телам приписывают одинаковую инертную массу.
22) Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нём деформаций.
23) Первый закон Ньютона постулирует наличие такого явления, как инерция тел. Поэтому он также известен как Закон инерции. Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения тела, на него необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью. Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела.
Второй
закон Ньютона — дифференциальный закон
движения,
описывающий взаимосвязь между приложенной
кматериальной
точке силой и
получающимся от этого ускорением этой
точки. Фактически, второй закон Ньютона
вводит массу как меру проявления
инертности материальной точки в выбранной
инерциальной системе отсчёта (ИСО).
![]()
Третий
закон объясняет, что происходит с двумя
взаимодействующими телами. Возьмём для
примера замкнутую систему, состоящую
из двух тел. Первое тело может действовать
на второе с некоторой силой ![]() ,
а второе — на первое с силой
,
а второе — на первое с силой ![]() .
Как соотносятся силы? Третий закон
Ньютона утверждает: сила действия равна
по модулю и противоположна по направлению
силе противодействия. Подчеркнём, что
эти силы приложены к разным телам, а
потому вовсе не компенсируются.
.
Как соотносятся силы? Третий закон
Ньютона утверждает: сила действия равна
по модулю и противоположна по направлению
силе противодействия. Подчеркнём, что
эти силы приложены к разным телам, а
потому вовсе не компенсируются.
24) Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта, в которой справедлив первый закон Ньютона (закон инерции): все свободные тела (то есть такие, на которые не действуют внешние силы или действие этих сил компенсируется) движутся прямолинейно и равномерно или покоятся[1]. Эквивалентной является следующая формулировка, удобная для использования в теоретической механике
25) )Примеры сил в механике:
1.Силы упругости возникают в теле при его упругой деформации Fупр= - k·DX,
2. Силы трения возникают в плоскости соприкосновения тел и препятствуют их относительному движению. Причинами сил трения являются неровности поверхности и силы межмолекулярного взаимодействия. Трение играет как полезную, так и вредную роль.
3. Трение покоя возникает при попытках вызвать движение одного тела по поверхности другого. Пусть на некое тело А, находящееся на поверхности, действует внешняя сила F, направленная параллельно плоскости соприкосновения. Сила F такова, что не может привести тело в движение. Следовательно, на тело действует равная ей по величине и противоположная по направлению сила трения покоя. Если возрастает внешняя сила F, то возрастает и сила трения покоя. Всегда Fтр. покоя = - F, но имеет предельное максимальное значение, равное Fтр. макс = M·N где M - коэффициент трения, зависящий от материала и состояния поверхностей, N - сила нормального давления тела на опору, равная силе реакции опоры.
4.Трение скольжения возникает при скольжении одного тела по поверхности другого. Сила трения скольжения равна максимальной силе трения покоя Fтр = m·N. Она всегда направлена параллельно плоскости соприкосновения тел в сторону, противоположную возможному относительному перемещению тел.
5.
Гравитационные силы. Закон
всемирного тяготения, установленный
Ньютоном, утверждает: любые
две материальные частицы притягиваются
друг к другу с силой, пропорциональной
произведению их масс и обратно
пропорциональной квадрату расстояния
между ними.![]() , где G -
гравитационная постоянная. Эту
силу называют силой тяготения или
гравитационной силой. Закон всемирного
тяготения справедлив для точечных масс.
, где G -
гравитационная постоянная. Эту
силу называют силой тяготения или
гравитационной силой. Закон всемирного
тяготения справедлив для точечных масс.
6.
Сила тяжести - сила, с которой тело
притягивается к Земле. По закону
всемирного тяготения на поверхности
Земли на тело массой m действует
сила тяжести, равная ![]() , где M -
масса земли, R - радиус Земли. Если
на тело действует только сила притяжения,
то оно совершает свободное
падение.Согласно 2 закону Ньютона
ускорение свободного падения равно
, где M -
масса земли, R - радиус Земли. Если
на тело действует только сила притяжения,
то оно совершает свободное
падение.Согласно 2 закону Ньютона
ускорение свободного падения равно ![]() .
Очевидно, что Fт =
m·g.
.
Очевидно, что Fт =
m·g.
7.Сила Архимеда На тело погруженное в жидкость или газ действует выталкивающая сила, равная весу вытесненной жидкости FA = mж·g = rж·Vж·g где rж- плотность жидкости, Vж- объем вытесненной жидкости (который равен объему погруженной части тела), g -ускорение свободного падения
Архимедова сила направлена противоположно силе тяжести, поэтому вес тела в жидкости или газе оказывается меньше веса, измеренного в вакууме.
26,27) Принцип относительности галилея
Для изучения механических явлений надо выбрать ту или иную систему отсчета. В различных системах отсчета законы движения имеют, вообще говоря, различный вид. Если взять произвольную систему отсчета, то может оказаться, что законы даже совсем простых явлений будут выглядеть в ней весьма сложно. Естественно, возникает задача отыскания такой системы отсчета, в которой законы механики выглядели бы наиболее просто.
По отношению к произвольной системе отсчета пространство является неоднородным и неизотропным. Это значит, что если какое-либо тело не взаимодействует ни с какими другими телами, то, тем не менее, его различные положения в пространстве и его различные ориентации в механическом отношении не эквивалентны. То же самое относится в общем случае и ко времени, которое будет неоднородным, т.е. его различные моменты неэквивалентными. Усложнение, которое вносили бы такие свойства пространства и времени в описание механических явлений, — очевидно. Как, например, свободное (т.е. не подвергающееся внешним воздействиям) тело не могло бы покоиться: если скорость тела в некоторый момент времени и равна нулю, то уже в следующий момент тело начало бы двигаться в некотором направлении.
Оказывается, однако, что всегда можно найти такую систему отсчета, по отношению к которой пространство является однородным и изотропным, а время — однородным. Такая система называется инерциальной. В ней, в частности, свободное тело, покоящееся в некоторый момент времени, остается в покое неограниченно долго.
Мы можем теперь сразу сделать некоторые заключения о виде функции Лагранжа свободно движущейся материальной точки в инерциальной системе отсчета. Однородность пространства и времени означает, что эта функция не может содержать явным образом ни радиус-вектора г точки, ни времени t, т.е. L является функцией лишь скорости v. В силу же изотропии пространства функция Лагранжа не может зависеть также и от направления вектора v, так что является функцией лишь от его абсолютной величины, т.е. от квадрата v2 = v2:
L = L (v2). (3.1)
Ввиду независимости функции Лагранжа от г имеем ∂L/∂r = 0, и потому уравнения Лагранжа имеют вид
![]()
![]() =
0
=
0
откуда ∂L/∂v = const. Но поскольку ∂L/∂v является функцией только скорости, то отсюда следует, что и
v = const. (3.2)
Таким образом, мы приходим к выводу, что в инерциальной системе отсчета всякое свободное движение происходит с постоянной по величине и направлению скоростью. Это утверждение составляет содержание так называемого закона инерции.
Если наряду с имеющейся у нас инерциальной системой отсчета мы введем другую систему, движущуюся относительно первой прямолинейно и равномерно, то законы свободного движения по отношению к этой новой системе будут теми же, что и по отношению к первоначальной: свободное движение снова будет происходить с постоянной скоростью.
Опыт показывает, однако, что не только законы свободного движения будут одинаковыми в этих системах, но что и во всех других механических отношениях они будут полностью эквивалентными. Таким образом, существует не одна, а бесконечное множество инерциальных систем отсчета, движущихся друг относительно друга прямолинейно и равномерно. Во всех этих системах свойства пространства и времени одинаковы и одинаковы все законы механики. Это утверждение составляет содержание так называемого принципа относительности Галилея одного из важнейших принципов механики.
Все сказанное достаточно ясно свидетельствует об исключительности свойств инерциальных систем отсчета, в силу которых именно эти системы должны, как правило, использоваться при изучении механических явлений. Везде в дальнейшем, где обратное не оговорено особо, мы будем рассматривать только инерциальные системы отсчета.
Полная механическая эквивалентность всего бесчисленного множества таких систем показывает в то же время, что не существует никакой одной «абсолютной» системы отсчета, которую можно было бы предпочесть другим системам.
Координаты r и r’ одной и той же точки в двух различных системах отсчета К и К', из которых вторая движется относительно первой со скоростью V, связаны друг с другом соотношением
r = r' + Vt. (3.3)
При этом подразумевается, что ход времени одинаков в обеих системах:
t = t'. (3.4)
Предположение об абсолютности времени лежит в самой основе представлений классической механики.
Формулы (3.3), (3.4) называют преобразованием Галилея. Принцип относительности Галилея можно сформулировать как требование инвариантности уравнений движения механики по отношению к этому преобразованию.
29)
И́мпульс и масса (Количество
движения) — векторная физическая
величина, являющаяся мероймеханического
движения тела. В классической
механике импульс тела равен
произведениюмассы m этого
тела на его скорость v,
направление импульса совпадает с
направлением вектора скорости:![]() .
.
30) Механическая система и ее центр масс.
Механическая система - совокупность материальных точек (тел), рассматриваемых как единое целое.
Центр масс механичиской системы - воображаемая точка С, расположение которой характеризует распределение масс в системе.
Центр масс механической системы движется, как материальная точка, в которой сосредоточена вся масса системы и к которой приложены все силы действующие на систему.
Уравнение изменения импульса механической системы.
В
классической механике полным импульсом
системы материальных точек называется
векторная величина, равная сумме
произведений масс материальных точек
на их скорости:![]()
31) Теорема о движении центра масс системы
Пусть система будет неизменяемой. В этом случае ее называют абсолютно твердым телом или просто телом.
Уравнение движения твердого тела получим, сложив уравнения (16.1.1):
![]()
Рассмотрим левую часть уравнения. Следуя уравнению (15.2.1) можем записать:
![]()
Дважды продифференцировав по времени, найдем:
![]()
или
![]()
Левая часть найдена. В правой останется только сумма внешних сил, так как согласно (15.1.1) сумма внутренних сил равна нулю. Итак
![]()
Это аналитическое представление теоремы о движении центра масс системы.
Произведение суммарной массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил.
Проектируя уравнение (16.2.5) на оси координат, получим
![]()
то есть дифференциальные уравнения движения в проекциях. Значение теоремы о движении центра масс:
1. Решения, которые мы получаем, рассматривая данное тело как материальную точку, определяют закон движения центра масс этого тела.
2. Все внутренние силы можно исключить из рассмотрения.
32)Закон сохранения движения центра масс системы
Теорема о движении центра масс дает следующие следствия:
1. Если сумма действующих на систему внешних сил равна нулю
![]()
то центр масс системы движется равномерно и прямолинейно, то есть, при М = const:
![]()
2.
Пусть ![]() ,
тогда
,
тогда
![]()
Если сумма проекций внешних сил на какую-нибудь ось равна нулю, то проекция скорости центра масс системы на эту ось есть величина постоянная.
Эти два следствия выражают закон сохранения движения центра масс системы.
33) Движение тела переменной массы
В
некоторых случаях тел связано с изменением
их массы, например масса ракеты уменьшается
вследствие истечения газов, образующихся
при сгорании топлива, и т. п.
Произведем
вывод уравнения движения тела переменной
массы на примере движения ракеты. Если
в момент времени t масса ракеты m, а ее
скорость v, то по истечении времени dt ее
масса уменьшится на dm и станет равной
т-dm, а скорость станет равной v+dv. Изменение
импульса системы за промежуток времени
dt
![]() где
u - скорость истечения газов относительно
ракеты. Тогда
где
u - скорость истечения газов относительно
ракеты. Тогда
![]() здесь
учтено, что dmdv - малое высшего порядка
малости по сравнению с остальными
слагаемыми. Если на систему действуют
внешние силы, то dp=Fdt,
поэтому
здесь
учтено, что dmdv - малое высшего порядка
малости по сравнению с остальными
слагаемыми. Если на систему действуют
внешние силы, то dp=Fdt,
поэтому
![]() или
или
![]() (1)
Второе
слагаемое в правой части (1) называют реактивной
силой Fp.
Если u противоположен v по направлению,
то ракета ускоряется, а если совпадает
с v, то тормозится.
Таким
образом, мы получили уравнение движения
тела переменной массы
(1)
Второе
слагаемое в правой части (1) называют реактивной
силой Fp.
Если u противоположен v по направлению,
то ракета ускоряется, а если совпадает
с v, то тормозится.
Таким
образом, мы получили уравнение движения
тела переменной массы
![]() (2)
которое
впервые было выведено И. В. Мещерским
(1859-1935).
Рассмотрим
случай отсутвтия воздействия внешних
сил на ракету. Положим в уравнении (1)
F=0 и будем считать, что скорость
выбрасываемых газов относительно ракеты
постоянна (ракета движется прямолинейно),
получим
(2)
которое
впервые было выведено И. В. Мещерским
(1859-1935).
Рассмотрим
случай отсутвтия воздействия внешних
сил на ракету. Положим в уравнении (1)
F=0 и будем считать, что скорость
выбрасываемых газов относительно ракеты
постоянна (ракета движется прямолинейно),
получим
![]() откуда
откуда
![]() Значение
постоянной интегрирования С определим
из начальных условий. Если в начальный
момент времени стартовая масса m0,
а ее скорость ракеты равна нулю, то С =
uln(m0). Следовательно,
Значение
постоянной интегрирования С определим
из начальных условий. Если в начальный
момент времени стартовая масса m0,
а ее скорость ракеты равна нулю, то С =
uln(m0). Следовательно,
![]() Это
соотношение называется формулой
Циолковского.
Выражения
(2) и (3) верны для нерелятивистских
движений, т. е. для случаев, когда скорости
v и u малы по сравнению со скоростью света
в вакууме.
Это
соотношение называется формулой
Циолковского.
Выражения
(2) и (3) верны для нерелятивистских
движений, т. е. для случаев, когда скорости
v и u малы по сравнению со скоростью света
в вакууме.
34) Уравнение Мещерского — основное уравнение в механике тел переменной массы, полученное И. В. Мещерским дляматериальной точки переменной массы (состава)
Уравнение обычно
записывается в следующем виде:
![]()
где:
m — масса материальной точки переменной массы, меняющаяся за счет обмена частицами с окружающей средой;
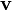 —
скорость
движения материальной
точки переменной массы;
—
скорость
движения материальной
точки переменной массы; —
внешние силы,
действующие на материальную
точку переменной массы со
стороны ее внешнего окружения (в том
числе, если такое имеет место, и со
стороны среды, с которой она обменивается
частицами, например электромагнитные
силы — в случае массообмена с
магнитной средой, сопротивление среды
движению и т. п.);
—
внешние силы,
действующие на материальную
точку переменной массы со
стороны ее внешнего окружения (в том
числе, если такое имеет место, и со
стороны среды, с которой она обменивается
частицами, например электромагнитные
силы — в случае массообмена с
магнитной средой, сопротивление среды
движению и т. п.); —
относительная
скорость присоединяющихся частиц;
—
относительная
скорость присоединяющихся частиц;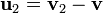 —
относительная
скорость отделяющихся частиц;
—
относительная
скорость отделяющихся частиц;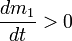 ,
, 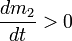 —
скорости массообмена присоединяющихся
и отделяющихся частиц;
—
скорости массообмена присоединяющихся
и отделяющихся частиц;
Формула Циолковского может быть получена как результат решения этого уравнения.
Уравнение Мещерского является следствием законов механики Ньютона (в частности, второго закона Ньютона) и ряда допущений о процессе движения материальной точки переменной массы . При этом величина:
![]()
