Неравенство Макмиллана:

_n

Sum (1/2^Si)<=1, где s_i – натуральные числа.

ⁱ⁼¹

Утверждение. Если схема разделима, то для длин ее элементарных кодов выполняется неравенство Макмиллана. Обратно, если для данного набора натуральных чисел выполняется неравенство Макмиллана, то существует разделимая схема, длины элементарных кодов которой равны данным числам.

Задание. Код Морзе - неразделимая схема. Доказать.

Пример префиксного кодирования чисел - код Левенштейна для натуральных чисел.

Двоичная запись натуральных чисел не является префиксной. Этот недостаток ликвидируется кодированием Левенштейна.

Введем вспомогательные понятия:

1. Определим рекурсивную последовательность натуральных чисел: n(0),n(1),n(2),n(3),…

По определению: n(0)=0; n(i)=2^n(i-1) для i>0.

Таким образом, имеем: n(0)=0, n(1)=1, n(2)=2¹=2, n(3)= 2²=4, n(4)= 2⁴=16, n(5)= 2ⁿ⁽⁴⁾=2¹⁶

2. На множестве натуральных чисел определим функцию log* :

log*x=i, где n(i)<=x< n(i+1)

Например, log*100=4, log*2¹⁰⁰=5, т.к. n(5)<=2¹⁰⁰<n(6)

3. Bin’x – бинарная запись числа x без первой 1.

Например, Bin`129=0000001, т.к. 129=10000001.

Утверждение. |Bin’x|=[log₂x], где |Bin’x| - длина слова Bin’x, [log₂x]-целая часть log₂x.

Примечание. log₂x – логарифм по основанию 2 от x.

Обозначим код Левенштейна натурального числа x как Lev(x).

Код Левенштейна формируется справа налево.

Алгоритм построения кода Левенштейна:

1. Выпиши Bin’x.

2. Припиши слева (log*x-1) итераций Bin’[log₂⁽ⁱ⁾x], i=1,2,…, log*x-1.

Пояснение. log₂⁽ⁱ⁾x= log₂(…(log₂(log₂x))…)

i раз

3. Припиши слева 0.

4. Припиши слева log*x единиц.

в итоге получаем следующую «схему» кода Левенштейна натурального числа x:

11…1 0 Bin’[log₂⁽ⁱ⁾x] … Bin’[log₂x] Bin’x

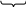
d c b a

Пример. x=37

log*37=4; [log₂37]=5 [log₂⁽²⁾37]=2 [log₂⁽³⁾37]=1 =>

Bin’1=пусто. Bin’2=0, Bin’5=01 Bin’37=00101 => Lev(37)=1111 0 0 01 00101

Утверждение. В коде Левенштейна каждое подслово является укороченной на одну цифру(единицу) бинарной записью длины следующего слова. Это не относится к начальному подслову 11…10, по которому можно узнать сколько раз приписывается слово Bin’[log⁽ⁱ⁾x].

Это утверждение определяет алгоритм декодирования кода Левенштейна.

Пример. Пусть начальный отрезок последовательности кодов Левенштейна имеет вид:

111100100010111101001…

Декодируем:

1. слева 4 единицы => log*x=4

2. считываем первую цифру после первого нуля – 0, приписываем к ней 1 => 1Bin’[log₂⁽²⁾x]=10=2

3. Берем 2 последующие цифры, приписываем слева 1 => 1Bin’[log₂⁽¹⁾x]=110=6

4. Приписывая слева 1 к последующим 6 цифрам получаем 1Bin’x=1001011=75 => x=75.

Пример. Расшифровать 11110 0 10 000001 [ответ-Lev(65)], 11110 0 11 0000010 [ответ-Lev(130)], 11110 1 000 00000001 [ответ-Lev(257)]

$1.4. Задача создания оптимального префиксного кода.

Сжатие информации это процесс сокращения количества бит, необходимых для хранения некоторого объема информации.