5 Методические указания по расчету динамических параметров системы

Исходя из задания для курсового проектирования:

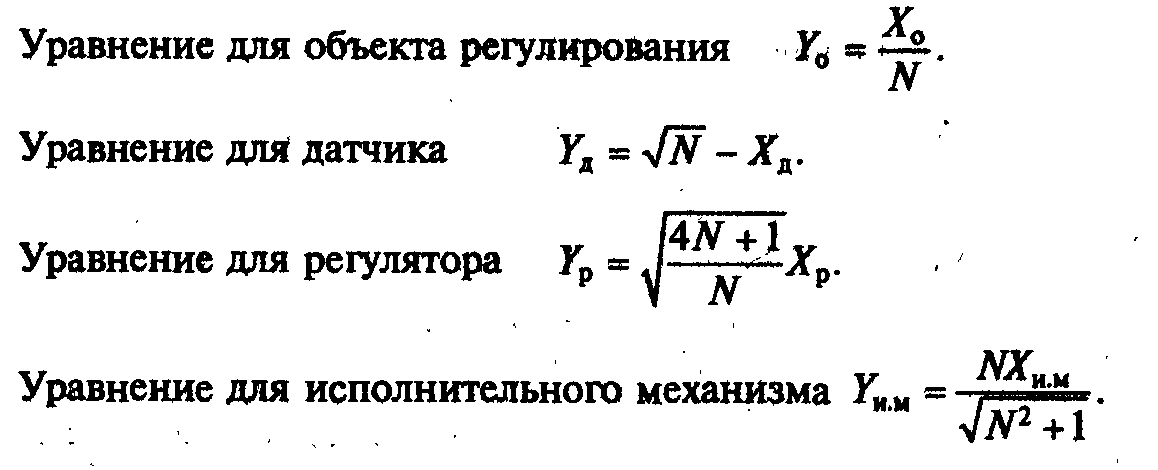
Для определения передаточной функции всей системы необходимо подобрать передаточные функции датчика, регулятора, исполнительного механизма (Горошков Б.И. Автоматическое управление: Учебник для студ. учреждений сред.проф.образования/ -М.: ИРПО:Издательский центр «Академия», 2003. – 304с стр.279 – 280). Затем вычисляем передаточные функции для N, заданного преподавателем.

Структурную схему системы преобразуем к виду:

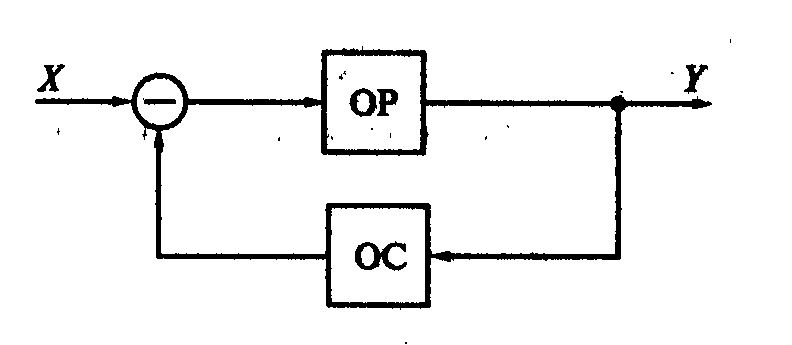
Для определения передаточной функции обратной связи Wос необходимо воспользоваться формулой

Для определения передаточной функции системы воспользуемся выражением:

Для нахождения временной функции переходного процесса необходимо упростить полученное выражение: из числителя необходимо исключить слагаемые, содержащие р в степени

больше 1, из знаменателя исключаются слагаемые, содержащие р в степени больше 2.

Для определения переходной функции представим общее выражение в виде двух слагаемых. Эти слагаемые можно получить, если определить корни характеристического уравнения

Где р₁ и р₂ – значения корней характеристического уравнения.

Для определения корней характеристического уравнения приравняем к нулю знаменатель и решим квадратное уравнение.

Затем необходимо определить значения коэффициентов А и В.

Для определения функций времени необходимо воспользоваться обратным преобразованием Лапласа:

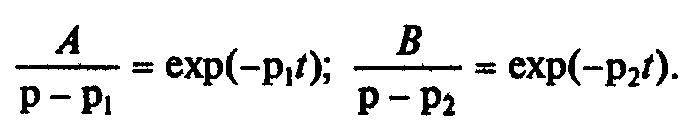
Подробные преобразования приведены в (Горошков Б.И. Автоматическое управление: Учебник для студ. Учреждений сред.проф.образования/ -М.: ИРПО:Издательский центр «Академия», 2003. – 304с стр.287 – 289).

Затем, используя программу Excel, строится график переходного процесса h(t).

Из полученного графика определяем время регулирования tрег.

6 Методические указания по определению устойчивости системы автоматического регулирования

Устойчивость системы определим двумя способами:

1. метод Гурвица

2. по кривой годографа (метод Найквиста).

6.1 Определение устойчивости системы автоматического регулирования методом Гурвица.

Алгебраические критерии устойчивости позволяют судить об устойчивости и неустойчивости системы непосредственно по коэффициентам характеристического полинома без вычисления его корней. В ТАУ наибольшее применение получили критерии Гурвица и Рауса.

Критерий устойчивости Гурвица:

Для устойчивости линейных систем необходимо и достаточно, чтобы при положительности всех коэффициентов характеристического полинома все главных определителей матрицы Гурвица были положительны.

Матрица Гурвица обозначена буквой « » и имеет вид

Условие положительности главных определителей

Гурвициана

(

Для определения устойчивости по критерию Гурвица, необходимо вернуться к характеристическому уравнению всей системы, полученному в п.1.2 (полное уравнение).

Составляется матрица, определяются главные определители, после чего делается заключение об устойчивости системы.