16 Вопрос Компонентные и топологические уравнения электрической подсистемы
Типовыми простейшими элементами электрической подсистемы являются электрическое сопротивление R, электрическая емкость С и электрическая индуктивность L. При описании их функционирования используются фазовые переменные типа потока (сила тока I) и типа потенциала (напряжение U). Значение напряжения на этих элементах совпадает с разностью значений электрического потенциала на концах элементов, напряжение на элементе источника тока равно его ЭДС.
Согласно основным законам электротехники компонентные уравнения этих типовых элементов соответственно имеют вид:
;
;
.
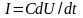Уравнения равновесия (первый закон Кирхгофа) и непрерывности (второй закон Кирхгофа), устанавливающие равенство нулю суммы токов в узлах схемы и суммы напряжений на элементах схемы при их обходе по произвольному контуру, дают топологические уравнения подсистемы
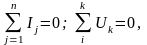
где n – число ветвей в узле схемы; k – число элементов в контуре схемы.
17 Вопрос Компонентные и топологические уравнения механической подсистемы(поступательное и вращательное).
Типовыми
элементами этих подсистем являются
элементы трения, элементы массы и упругие
элементы. В качестве фазовых переменных
выступают сила
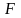и скорость v
– для поступательной подсистемы и
момент
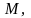угловая скорость
– для вращательной.
Математические модели элементов трения получаются из уравнений вязкого трения:
,
где
и k
– коэффициенты диссипации соответственно
для поступательной и вращательной
подсистем; vот,
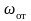– относительные скорости контактируемых
тел.
Введем
понятия механического сопротивления
при поступательном движении
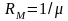и вращательном
.
Тогда
.
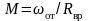Математическую модель массы выражает второй закон Ньютона:
F
=
/dt;
M
= Jd
/dt,
где m – масса элемента; J – момент инерции массы относительно ее оси вращения.
Математическая модель упругого элемента получается из закона Гука. Для поступательной подсистемы
,
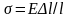где
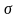и
– соответственно напряжение и удлинение
стержня в продольном направлении; Е –
модуль упругости первого рода; l
– начальная длина стержня.
Так как = F/S, где S – площадь поперечного сечения стержня, после дифференцирования по времени получим
dF/dt = SEvот/l = сvот или vот = (1/c)(dF/df ) = LМ dF/dt,
где с
– жесткость; vот
= dl/dt
– скорость деформации;
=
1/с – податливость.
Для
вращательной системы при закрутке вала
на угол
получаем аналогичное компонентное
уравнение
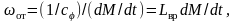
где
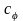– крутильная жесткость;
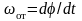– угловая скорость деформации;
– крутильная податливость.
Топологические уравнения подсистемы получаются из уравнений равновесия (принцип Д'Аламбера) и уравнений непрерывности (сумма абсолютной, переносной и относительной скоростей равна нулю):
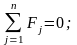
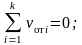
Особенностью механической поступательной системы является то, что в топологических уравнениях фигурируют не алгебраические, а геометрические суммы. Другими словами, топологические уравнения в виде алгебраических сумм должны записываться для проекций сил и скоростей на каждую ось координат.