15 Вопрос компонентные и топологические уравнения элементов и систем

Основными методами создания ММ на макроуровне являются инвариантные методы. Они предполагают разбиение всей системы на отдельные элементы, описание свойств каждого элемента на уровне взаимодействия их между собой с помощью ММ и последующее объединение их в единую структуру на основе связей между фазовыми переменными. Процедура выделения элементов выполняется человеком, а составление общей системы уравнений для полученной структуры объекта – ЭВМ.

Математические модели элементов получают одним из способов, рассмотренных выше. Уравнения, входящие в ММ элементов, называются компонентными. Они отражают законы функционирования элемента и связывают разнородные фазовые переменные, относящиеся к этому элементу. Так, уравнение второго закона Ньютона связывает силу и ускорение. Уравнения могут быть алгебраическими или дифференциальными, линейными или нелинейными.

Для объединения элементов в систему используются топологические уравнения. Они отражают способ связи элементов между собой в составе системы. Топологические уравнения могут выражать законы сохранения, условия неразрывности, равновесия и т. п. Топологические уравнения связывают однотипные фазовые переменные, относящиеся к разным элементам системы, их получают на основе сведений о структуре системы. Рассмотрим пример одномассовой колебательной системы. Пусть требуется, например, определить вертикальные ускорения на месте водителя транспортного средства, если известен закон вертикального перемещения остова трактора в месте установки подрессоренного сиденья. Задача может быть решена с использованием одномассовой схемы динамической системы, показанной на рис. 9.1. Здесь масса сиденья и водителя т выделена в отдельный инерционный элемент, связанный с внешней средой посредством двух элементов, учитывающих упругие с и демпфирующие 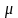свойства сиденья. Рассмотрим движение системы вдоль вертикальной оси x, совершающей перемещение в горизонтальном направлении совместно с остовом.

Рис. 9.1. Схема одномассовой механической системы

Фазовыми переменными для инерционного элемента являются сила инерции F_m и перемещение х_т, а компонентное уравнение имеет вид:

где t – текущее время (независимая переменная).

Для упругого элемента фазовыми переменными являются сила упругости 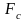и деформация 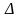, а компонентное уравнение имеет вид:

.

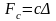Здесь внутренний параметр с – жесткость упругого элемента.

Фазовыми переменными элемента сопротивления будут сила сопротивления амортизатора F_R и скорость деформации a внутренним параметром – коэффициент демпфирования . Компонентное уравнение имеет вид:

.

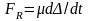Источником колебаний системы являются вертикальное перемещение кузова х_к (фазовая переменная источника), закон изменения которого известен: х_к = х_к(t).

Для получения ММ объекта необходимо полученные компонентные уравнения дополнить топологическими. Согласно схеме динамической системы (рис. 9.1) и принципу Д'Аламбера

.

Из уравнения непрерывности

.

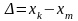Решение системы этих уравнений при выбранных значениях коэффициентов и законе перемещения остова позволяет определить вертикальное ускорение на месте водителя am = d ²x_m /dt² для любого момента времени.

В качестве фазовой переменной в механических системах часто используется не перемещение, а скорость, поэтому компонентные и топологические уравнения рассматриваемой системы могут иметь несколько иной вид.

Для большинства ТО можно выделить три типа простейших элементов: элемент диссипации, преобразующий энергию соответствующего данной подсистеме вида в теплоту, и элементы, накапливающие потенциальную или кинетическую энергию.

Аналогию компонентных и топологических уравнений удобно проводить на основе электрической подсистемы. Рассмотрим использование аналогий на примерах подсистем, наиболее характерных для трактора и автомобиля – механической, гидравлической (пневматической), тепловой и электрической.