6 Вопрос .Функциональная мм механизма вывешивания адаптера (мва)

П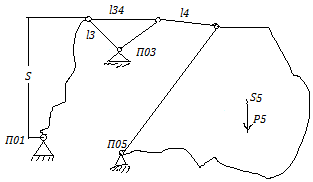 роблема копирования опорной поверхности имеет 2 неприятные стороны методами: галопирования, возникающие из-за недостаточного давления башмака на опорную поверхность; избыточное давление башмаков на ту же самую поверхность, котораяприводит к разрушению поверхностного слоя. МВА предназначен для мобильного энергоносителя обеспечивающей давление башмаков адаптера в заданных пределах 200-600Н. Большинство пространств МВА обладает симметрией и могут быть спровоцированы. Плоский аналог пространственного МВА представляет собой одноподвижный шестизвенник. Вертикальная координата точки контакта башмака с опорной поверхностью постоянного изменяется. Аналитическое исследование плоского аналога выполняется по методу Зеновьего. Исследование проводят по 4-х звенникам. Определение координат подвижных звеньев и характерных точек. W=3n-2p5/ Пружинные блоки предназначены для компенсации большей части веса адаптера.

Вопрос 40 оценка параметров регрессионной модели

Исходными данными для получения оценок параметров РМ технической системы (т. е. оценок искомых коэффициентов регрессии ) является информация о значениях управляемых факторов X и функции отклика . Эту информацию можно представить в виде матрицы X значений факторов во всех N опытах, предусмотренных спектром плана эксперимента, и вектора-столбца полученных в этих опытах значений функции отклика :

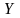где X_i = (X_il, X_i2,..., X_in) – вектор-строка значений факторов в i-м опыте; Х_ij – значение j-го фактора в i-м опыте; п – количество факторов; N – количество опытов; y_i – значение функции отклика в i-м опыте (если проводились параллельные опыты, т. е. дублирование опытов, то вместо y_i используются оценки их математических ожиданий, т. е. выборочные средние ).

Значения базисных функций во всех опытах представляют собой матрицу F, называемую матрицей базисных функций:

где – значение k-й базисной функции в i-м опыте; – вектор-строка значений базисных функций в i-м опыте.

Используя информацию об X, и F, необходимо найти оценки коэффициентов регрессии, представляемые вектором-столбцом

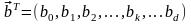, (19.1)

где b_k – значение оценки коэффициента регрессии при базисной функции f_k(X).

Так как функция отклика – случайная величина, поскольку на ее значения в различных опытах оказывает влияние случайная помеха , то оценки коэффициентов регрессии будут случайными величинами.

Уравнение регрессии устанавливает зависимость между оценкой математического ожидания функции отклика и факторами 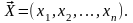Общий вид этой зависимости:

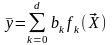. (19.2)

В связи с наличием помехи значение функции отклика в i-м опыте y_i будет отличаться от . Для определения y_i можно составить выражение

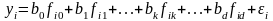, (19.3)

где 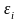– невязка уравнения регрессии в i-м опыте.

Невязка характеризует отклонение значений функции отклика в опытах от получаемых с помощью РМ (19.2). Она возникает по двум причинам: из-за ошибки эксперимента и из-за непригодности (приближенности) выбранной структуры ЭФМ. Причем эти причины смешаны, и нельзя сказать, какая из них преобладает.

Если постулировать, что модель пригодна, то невязка будет порождаться только ошибкой опыта. Тогда для определения коэффициентов уравнения (19.2) невязку надо минимизировать. Для этого в регрессионном анализе используется метод наименьших квадратов (МНК). Составляется функция, представляющая собой сумму квадратов невязок, и осуществляется ее минимизация:

. (19.4)

Подставим значение из выражения (19.3):

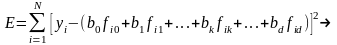min. (19.5)

В выражении (19.5) коэффициенты b_k рассматриваются как неизвестные переменные, которые наилучшим образом соответствуют полученным результатам эксперимента. Значения этих коэффициентов, при которых достигается минимум функции Е, принимаются в качестве оценок коэффициентов регрессии. Минимум функции Е имеет место при равенстве нулю частных производных этой функции по переменным :

\
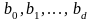
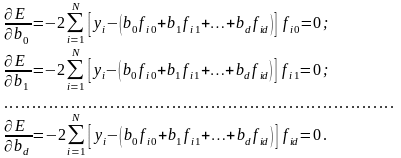