45 Вопрос план дробного факторного эксперимента

При построении ЭФМ, использующих упрощенные уравнения регрессий, когда N > N_B, применяют дробные факторные эксперименты (ДФЭ). Наибольшее распространение имеют регулярные планы ДФЭ типа , т. е. ДФЭ , где п – число факторов, р – степень дробности ДФЭ. Планы ДФЭ принято называть репликами с указанием их степени дробности. Так, план ДФЭ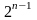 называют полурепликой ПФЭ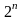 (1/2-реплика); ДФЭ 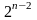– 1/4-реплика ПФЭ ; ДФЭ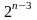 – 1/8-реплика ПФЭ и т. д. Полуреплика сокращает число опытов в два раза по сравнению с ПФЭ, 1/4-реплика – в четыре раза и т. д.

При построении матрицы спектра плана ДФЭ необходимо обеспечить выполнение условий, описываемых выражениями (22.8)–(22.11), принимая во внимание, что число точек спектра этого плана определяется по формуле

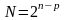. (23.2)

Условия (22.8)–(22.11) удовлетворяются, если в матрице базисных функций F отсутствуют полностью совпадающие или полностью противоположные столбцы, что позволяет получить раздельное оценивание всех коэффициентов регрессии.

При выборе степени дробности ДФЭ должно выполняться условие

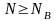. (23.3)

Выбранные базисные функции для ДФЭ составляют лишь некоторую часть базисных функций соответствующего ПФЭ. Назовем эти функции существенными переменными, характеризующими в наибольшей мере физические свойства ТО.

Процедура построения спектра плана ДФЭ содержит четыре этапа.

Этап 1. Выбор структуры уравнения регрессии и определение степени дробности ДФЭ. При этом исходят из условия выполнения соотношения (23.3).

Этап 2. Выбор ведущих факторов и построение для них матрицы спектра плана, определяющего программу их изменения в ходе эксперимента.

Число k ведущих факторов принимают равным разности между количеством факторов n и степенью дробности ДФЭ:

. (23.4)

Для выбранных ведущих факторов 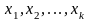строят план ПФЭ2^k, используя правило чередования знаков (см. тему 22).

Этап 3. Построение матрицы X спектра плана ДФЭ .

Часть этой матрицы составляет матрица спектра плана ПФЭ2^k, а во вторую часть должны войти столбцы матрицы для остальных факторов 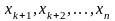, количество которых равно:

р = n – k. (23.5)

Столбцы матрицы X, соответствующие этим факторам, определяют путем перемножения соответствующих столбцов ведущих факторов. Для этого используют генерирующие соотношения. Генерирующим соотношением называется алгебраическое выражение, устанавливающее связь между одним из факторов и произведением какой-либо комбинации ведущих факторов x₁, x₂,..., x_k.

Этап 4. Проверка пригодности полученного спектра плана.

Для этого необходимо построить матрицу базисных функций F и проверить, нет ли в ней совпадающих или полностью противоположных столбцов, т. е. выяснить, обладает ли матрица F свойством ортогональности столбцов, определяемым выражением (22.9). Если в матрице F нет совпадающих или противоположных столбцов, полученный спектр плана ДФЭ пригоден для решения поставленной задачи. В противном случае выполняются последовательно следующие процедуры до тех пор, пока не будет обеспечена ортогональность: выбираются иные генерирующие соотношения; изменяется набор ведущих факторов; уменьшается степень дробности плана р.

Поскольку планы ДФЭ значительно экономичнее планов ПФЭ, они получили широкое практическое применение. В частности, их используют для анализа чувствительности целевой функции к вариации параметров ТО в процессе их отсеивания и отбора для осуществления оптимизации.