27 Вопрос использование уравнения лагранжа для моделирования динамических процессов в технических объектах

При моделировании сложных технических систем применяют уравнения Лагранжа второго рода. Их можно использовать при построении ММ ТО любой физической природы, если они рассматриваются как системы с сосредоточенными параметрами. При этом никаких ограничений на структуру и физические свойства объекта не накладывается.

Уравнения Лагранжа второго рода для системы с голономными связями имеют вид:

(12.1)

где Е_K – кинетическая энергия системы; 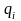– обобщенная координата; – обобщенная скорость; – обобщенная сила; п – число степеней свободы системы.

В качестве обобщенных координат выбирают независимые между собой переменные, которые позволяют полностью определить состояние исследуемой системы. Обычно в качестве обобщенных координат принимают величины, производные по времени от которых представляют собой фазовые координаты типа потока. Для механических систем обобщенными координатами выбирают линейные и угловые перемещения, а обобщенными скоростями – линейные и угловые скорости. В этом случае обобщенные силы сохраняют свой физический смысл и представляют собой силы и вращающие моменты.

Каждой обобщенной координате соответствует своя обобщенная сила . Работу всех обобщенных сил на возможных перемещениях системы (виртуальную работу) можно вычислить по формуле

(12.2)

где 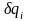– вариация i-й обобщенной координаты; – работа i-й обобщенной силы на возможном перемещении.

Из формулы (12.2) следует, что обобщенные силы представляют собой коэффициенты при вариациях обобщенных координат в выражении для виртуальной работы.

Математическая модель, получаемая на основе уравнений Лагранжа второго рода, представляет собой систему ОДУ вида

. (12.8)

В эту систему входит п дифференциальных уравнений второго порядка, где п – число степеней свободы системы.

Процедура получения ММ на основе уравнений Лагранжа второго рода включает следующие операции:

1) составление динамической модели ТО (при этом выделяются инерционные, упругие, диссипативные и другие элементы, определяются источники внешних воздействий);

2) определение возможных перемещений элементов системы с учетом наложенных позиционных голономных связей и введение обобщенных координат q_i, количество которых должно соответствовать числу степеней свободы системы п;

3) составление выражений для вычисления кинетической Е_к и потенциальной Е_П энергий и диссипативной функции Рэлея Ф;

4) составление выражения для вычисления виртуальной ра- боты источников внешних воздействий, определение обобщенных сил Q_i;

5) выполнение операций дифференцирования, предусмот-ренных уравнением (12.7), и формирование системы ОДУ.

Отметим важное свойство функций Е_К, Е_П и Ф – их аддитивность. Напомним, что способностью накапливать кинетическую энергию обладают инерционные элементы, а потенциальную энергию – упругие элементы. Диссипативные элементы рассеивают энергию системы, затрачивая ее на преодоление внутренних сопротивлений. В связи со свойством аддитивности кинетическая энергия системы равна сумме кинетических энергий всех инерционных элементов. Потенциальная энергия системы равна сумме потенциальных энергий всех упругих элементов, а диссипативная функция – сумме энергий потерь всех диссипативных элементов.

При плоском движении твердого тела кинетическая энергия равна сумме кинетических энергий в переносном (поступательном) и относительном (вращательном) движениях:

Е_к = 0,5mv² + 0,5Jω², (12.9)

где т – масса твердого тела; v – скорость центра масс тела; J – момент инерции твердого тела относительно оси, проходящей через центр масс; ω – угловая скорость вращения тела относительно этой оси.

Кинетическая энергия сосредоточенной массы жидкости в дискретном элементе – участке трубопровода

Е_к = 0,5m_ГQ², (12.10)

где т_Г – коэффициент массы, кг/м⁴; Q – расход, м³/с.

Кинетическая энергия дискретного инерционного элемента твердого тела при одномерной теплопередаче

Е_к = 0,5с_ТТ², (12.11)

где с_Т – теплоемкость инерционного элемента, Дж/К; Т – температура элемента, К.

Следует отметить, что Е_к в тепловой системе характеризует приращение кинетической энергии при нагреве на 1 К.

Кинетическая энергия инерционного элемента электрической системы

Е_к = 0,5LI², (12.12)

где L – индуктивность инерционного элемента, Гн; I – сила тока, А.

Потенциальная энергия упругого элемента

Е_П = 0,5сΔ², (12.13)

где с – параметр упругого элемента (характеризует его способность накапливать потенциальную энергию);

Δ = q₁ – q₂; q₁, q₂ – обобщенные координаты инерционных элементов, соединяемых данным упругим элементом.

Для механической системы Δ представляет собой величину деформации упругого элемента (линейную или угловую), для гидравлической – изменение объема жидкости упругого элемента, для электрической – изменение заряда конденсатора. Тепловая система упругими свойствами не обладает.

Диссипативная функция определяется по формуле

, (12.14)

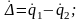
где – параметр диссипативного элемента; – обобщенные скорости (фазовые переменные типа потока), характеризующие состояния инерционных элементов, соединяемых данным диссипативным элементом.

Для механической системы представляет собой относительную скорость движения взаимодействующих сосредоточенных масс, для гидравлической – скорость движения сосредоточенной массы жидкости в дискретном участке трубопровода, в тепловой системе – разность температур в узлах дискретизации, в электрической – ток резистора.