
Варіанти завдань
Варіант |
Функції |
Варіант |
Функції |
Варіант |
Функції |
Варіант |
Функції |
1 |
1, 3 |
6 |
3, 4 |
11 |
3, 6 |
16 |
1, 5 |
2 |
2, 4 |
7 |
5, 6 |
12 |
1, 4 |
17 |
4, 5 |
3 |
5, 7 |
8 |
1, 2 |
13 |
2, 5 |
18 |
6, 7 |
4 |
2, 6 |
9 |
4, 7 |
14 |
4, 6 |
19 |
2, 7 |
5 |
1, 7 |
10 |
3, 7 |
15 |
2, 3 |
20 |
1, 6 |
Приклад 2.1
Нехай дано наступні експериментальні дані:
(x1; y1) |
(x2; y2) |
(x3; y3) |
(x4; y4) |
(x5; y5) |
(1; 1) |
(2; 2) |
(3; 3) |
(4; 4) |
(5; 5) |
Виконаємо апроксимацію функції методом найменших квадратів.
Апроксимація класичним методом
Згідно методу найменших квадратів Гауса сума S квадратів відстаней повинна бути мінімальною, тобто:
![]()
Сума S має екстремум в точці, де частинні похідні від коефіцієнтів дорівнюють нулю. Для нашої конкретної функції маємо:
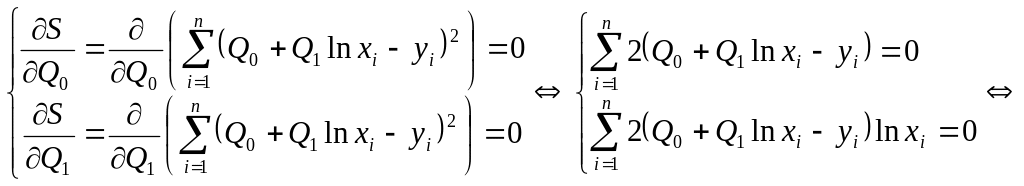

Отримали звичайну лінійну систему з двома невідомими. Для її розв’язання спершу розрахуємо коефіцієнти системи.
Таблиця 3
№ точки |
x |
y |
ln(x) |
ln2(x) |
y*ln(x) |
1 |
1 |
1 |
0 |
0 |
0 |
2 |
2 |
2 |
0,693147 |
0,480453 |
1,386294 |
3 |
3 |
3 |
1,098612 |
1,206949 |
3,295837 |
4 |
4 |
4 |
1,386294 |
1,921812 |
5,545177 |
5 |
5 |
5 |
1,609438 |
2,59029 |
8,04719 |
Сума |
|
15 |
4,787492 |
6,199504 |
18,2745 |
Тепер розв’яжемо дану систему за допомогою формул Крамера:
![]()
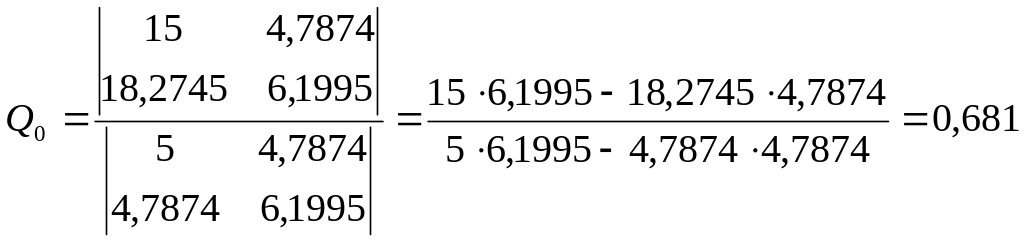
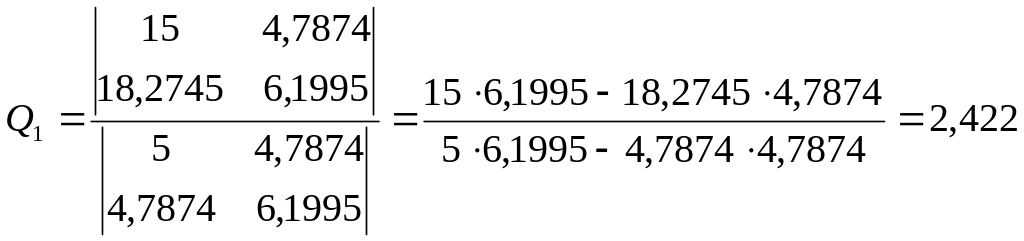
Отже, шукана апроксимуюча функція має наступний вигляд:
![]()
Апроксимація за допомогою пакету Mathcad
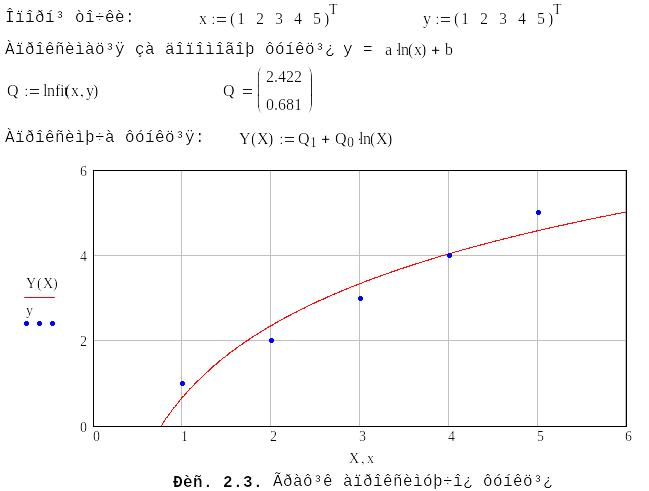
Приклад 2.2
Дано наступні експериментальні дані:
(x1; y1) |
(x2; y2) |
(x3; y3) |
(x4; y4) |
(x5; y5) |
(1; 0,1) |
(2,7; 1,5) |
(3,5; 2,5) |
(4,5; 3) |
(5; 6) |
Потрібно
виконати апроксимацію функції
![]() методом найменших квадратів.
методом найменших квадратів.
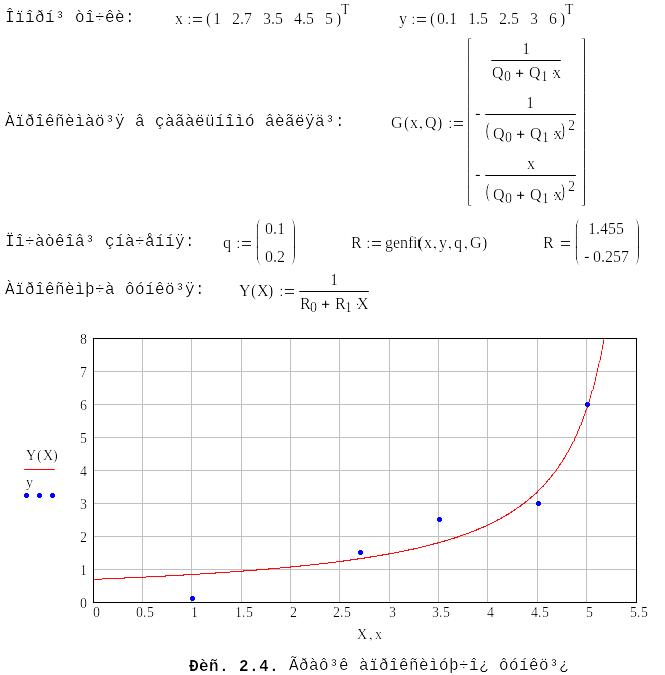
Оскільки в MathCad 2001і немає відповідної функції для апроксимації, то застосуємо апроксимацію в загального вигляді.
Функція genfit(x, y, g, G) повертає вектор параметрів, що реалізують регресію даних за допомогою функції користувача загального вигляду:
x – вектор дійсних даних аргументу;
y – вектор дійсних значень того ж самого розміру;
g – вектор початкових параметрів апроксимації розмірності N;
G(x, С) – векторна функція розмірності N+1, що складається з функції користувача і її N частинних похідних по кожному із параметрів С.
Знайдемо частинні похідні для даної функції:
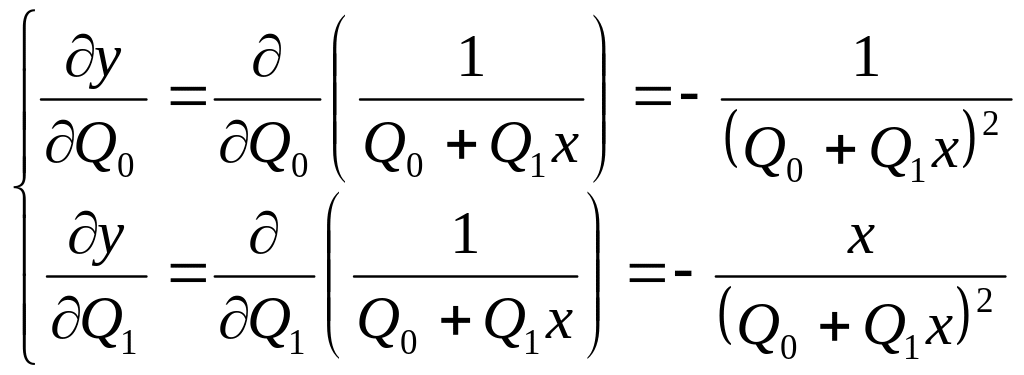
Звіт повинен містити
Тему та мету роботи.
Вихідні дані із табл. 2.
Короткі теоретичні відомості та методи, які використовуються в лабораторній роботі.
Апроксимацію однієї функції методом найменших квадратів класичним способом (вручну) для одного з набору даних.
Графіки апроксимованих функцій з відповідними опорними точками.
Висновки по результатам виконаної роботи.
Запитання для контролю
Що таке апроксимація? Чим вона відрізняється від інтерполяції?
Які існують види інтерполяції та апроксимації?
В чому сутність апроксимації за методом найменших квадратів?
Як виконати апроксимацію за допомогою пакету Mathcad?
Що таке апроксимація в загальному вигляді? Коли її доцільно застосовувати?
