Лабораторна робота №6-7 Апроксимація функцій методом найменших квадратів

Мета: навчитися розраховувати параметри апроксимуючих функцій методом найменших квадратів.

Короткі теоретичні відомості

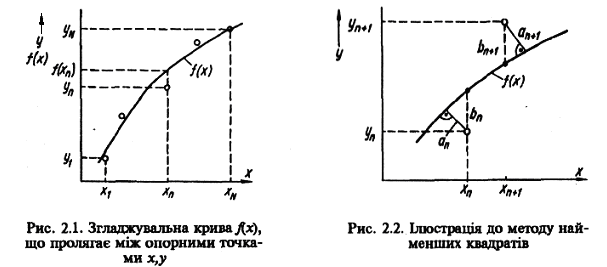
При інтерполяції шукана крива f(х) проходить через опорні точки f(х_n) = у_n. Знайдена функція дає змогу обчислювати вихідний сигнал f(х) також і між опорними точками х_n  х  х_n+1. При ап­роксимації шукану криву треба провести за деякою визначеною стра­тегією між парами значень (розсіяними чи зашумленими), не досягаючи того, щоб на опорних точках значення функції збігалися з виміряними значеннями у_n (рис. 2.1).

За допомогою функції, яку задають формулою, можна:

1. описувати кількісно виміряний ефект;

2. заносити характеристику в пам'ять ЕОМ;

3. обчислювати й видавати значення абсциси, яке належить відповідному значенню ординати;

4. проводити подальшу обробку аналітично заданої функції, наприклад диференціювати або інтегрувати.

Узгоджувати згладжувальну криву f(х) з парами вимірювань х_n, у_n можна різними методами:

а) сума абсолютних різниць |f(х_n)-у_n| повинна наближатися до мінімуму; абсолютна норма мінімізується, й відбувається лінійна L₁ апроксимація:

, (2.1)

б) сума квадратів різниць повинна наближатися до мінімуму; мінімізується евклідова норма. Цей метод найменших квадратів Гаусса називається квадратичною L ₂-апроксимацією:

, (2.2)

в) максимальна різниця між згладжувальною кривою та виміря­ною величиною повинна залишитися в межах D у разі апроксимації Чебишова або L_ – апроксимації мас місце:

, (2.3)

У подальшому застосовуватимемо виключно метод найменших квадратів, який порівняно з мінімізацією абсолютної норми зручніший для використання. Крім того, до компенсації будемо звертатися, якщо похибки вимірювань розподілені нормально. Апроксимація Чебишова раціональна тоді, коли трансцендентна функція (тригоно­метрична, логарифмічна) аналітично задана на деякому інтервалі й може бути наближена за допомогою простого в обчисленні полінома.

Строго кажучи, при методі найменших квадратів необхідно міні­мізувати перпендикулярні відстані виміряних точок х_n,, у_n до шуканої кривої (рис.2.2). На це в подальшому не звертатимемо уваги. Абсциси розглядатимемо як практично вільні від похибок, а мінімізуватимемо лише вертикальні відстані, тобто різниці ординат f(х_n) - у_n.

Якщо згладжувальна крива відома, то можна обчислити різниці ординат та їхній статистичний розподіл. Згладжувальна крива тільки тоді достатньо точно відповідає характеристиці, коли стандартне відхилення розподілу різниць приблизно збігається з точністю виміряної величини.

Апроксимуючий поліном. Апроксимуючі криві за винятком періодичних сигналів у загальному випадку монотонне низхідні чи монотонне висхідні. Екстремуми не очікуються, оскільки тоді характеристика багатозначна. Крім того, не розглядатимуться коливання, які накладаються на характеристику. Отже, для згладжування треба відшукати поліноми не вище третього ступеня, тобто прямі, квадратичні та кубічні параболи. У загально­му випадку згладжувальний поліном Р(х) буде мати вигляд:

, (2.4)

Для аргументу х_n значення полінома Р(х_n). Воно в загальному випадку відрізняється від виміряної величини у_n. Різниця ординат, відстань або залишок r дорівнює:

, (2.5)

Для l  n  N маємо N пар вимірів. За методом найменших квадратів Гауса сума S квадратів залишків або відстаней повинна бути мінімальною. При необхідності квадрати відстаней будуть ще зва­жені за допомогою вагової функції. У цьому разі:

, (2.6)

Проте надалі обчислення будуть вестися при w(х_n) = 1. Сума S квадратів відстаней є функцією шуканих коефіцієнтів полінома S= S(а,b,с,d). Сума S має екстремум у точці, де частинні похідні від коефіцієнтів дорівнюють нулю:

, (2.7)

Цей екстремум є мінімумом, оскільки матриця інших похідних від коефіцієнтів завжди позитивна. Тим самим із початкової формули (2.4) утворюються чотири рівняння для чотирьох невідомих а,b,с,d.

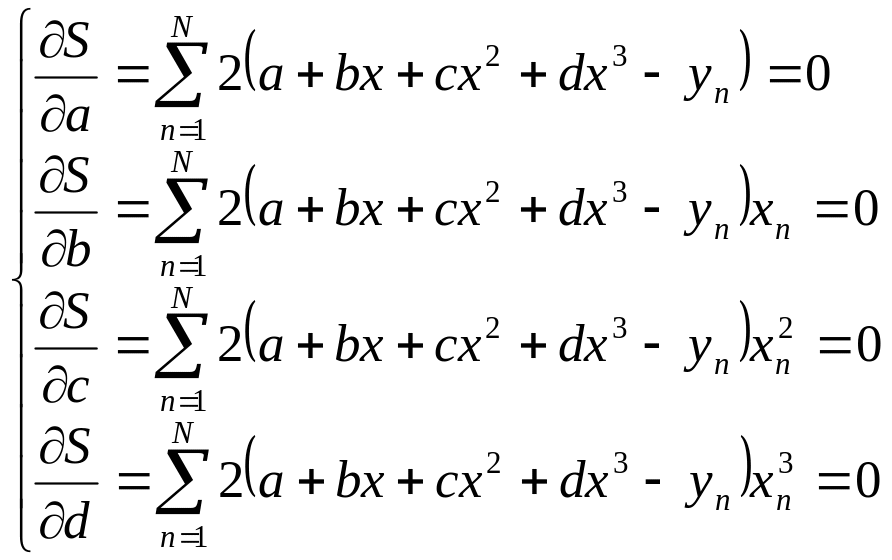, (2.8)

Розкриваючи дужки та переміщуючи у_n праворуч, дістанемо систему звичайних лінійних рівнянь, розв’язавши яку отримаємо коефіцієнти поліному.

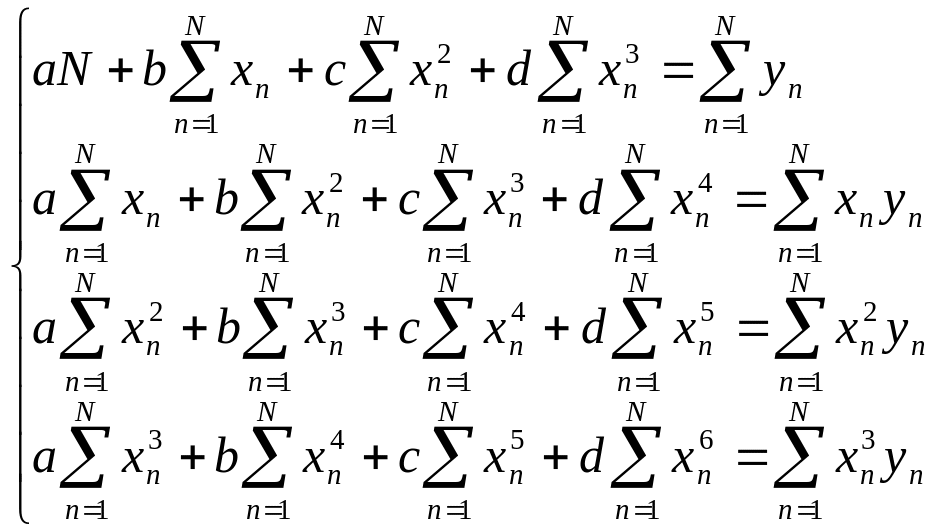, (2.9)

Розглянемо згладжувальну пряму. Вираз (6.4) справедливий і при прямій характеристиці. У цьому разі коефіцієнти с і А дорівнюють нулю. Проте доцільно при дослідженні лінійного зв'язку апроксимуючий поліном задавати одразу як пряму:

, (2.10)

Із (2.9) залишаються тільки нормальні рівняння:

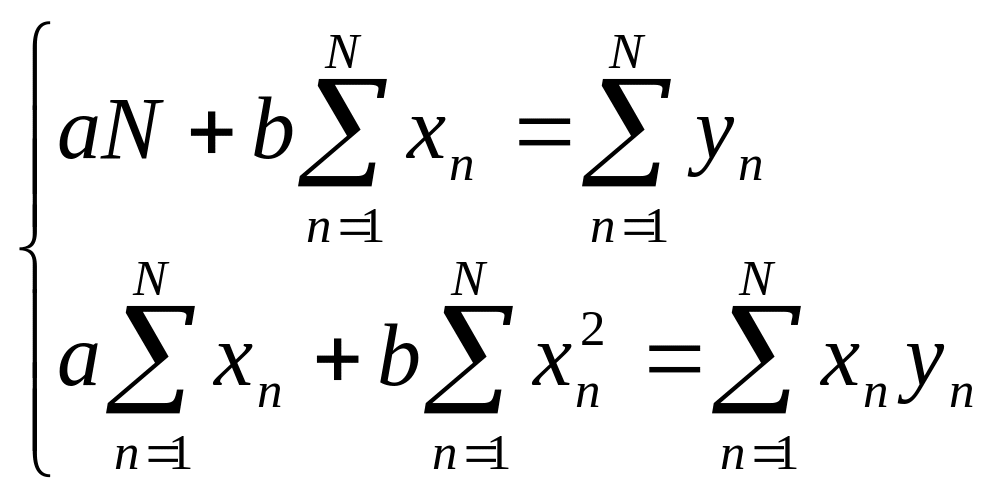, (2.11)

Систему (2.11) розв'язують відносно а і b, отримуючи шукану пряму:

, (2.12)