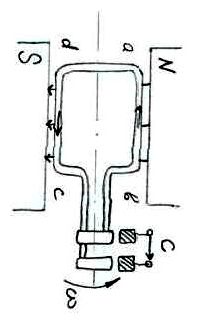
2.1 Получение синусоидальной эдс. Основные величины
Эл. цепи, в которых значения и направления ЭДС, напряжения и тока периодически изменяются по sin-ому закону наз цепями sin-го тока. Для получения sin-ой ЭДС можно использовать проводник в виде прямоугольной рамки, катушку, которая вращается со скоростью ω в постоянном магнит поле. Мгновенное значение перем-го тока в любой заданный момент времени, наз-ся мгн. знач. тока.
- мгновенное значение тока
Синусоидальный ток характеризуется следующими параметрами:
О
сновные
величины, характеризующие гармонические
колебания.
a(t) = Am sin (ωt + ψ0), где Am – амплитуда ; ω – угловая частота колебаний ; ψ – частота колебаний;
T = 1/t - период колебаний; ψ0 – начальная фаза колебаний ; ωt + ψ0 – текущая фаза колебаний
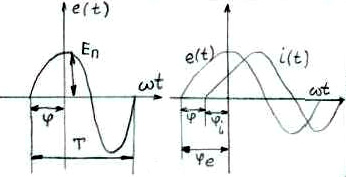
В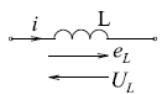
цепях переменного тока напряж и ток
явл-сь синусоид-ой измен-щейся с одиноковой
частотой имеют разные начальные фазы
колебаний. Разность м/у нач. фазами
напряжения и тока наз. сдвигом фаз м/у
напряжением и током.
2.2 Представление синусоидальных функций в различных формах.
1. Аналитический способ
u(t) = Um sin (ωt + ψu)
е(t) = Еm sin (ωt + ψe)
i(t) = Im sin (ωt + ψi)
Но для расчета электрических цепей такое выражение неудобно, т.к. алгебраические действия с тригонометрическими функциями приводят к громоздким вычислениям
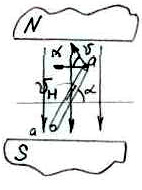
2. Представление синусоидальных функций при помощи векторов
Позволяет наглядно показать количественные и фазовые соотношения в цепях синусоидального тока. Векторы изображаются неподвижными для t=0. Длина вектора соответствует действующему значению. Углы наклона к оси абсцисс равны начальным фазам(ψi,ψu)
Неподвижные векторы определяют два параметра синусоидальной функции: действующее значение (амплитуду) и начальную фазу. Третий параметр – угловая частоты ω - должен быть известен
Угол между вектором напряжения и вектором тока равен углу сдвига фаз . Если и напряжение опережает по фазе ток на угол сдвига фаз . Если
И напряжение отстает по фазе от тока. Угол всегда откладывается от вектора тока I к вектору напряжения U
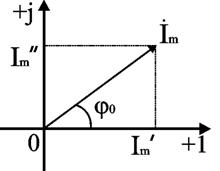
3. Представление синусоидальных функций при помощи комплексных чисел
На комплексной плоскости с осями координат +1 (ось действительных чисел и величин) и +j (ось мнимых чисел и величин) откладывают вектор Im под углом ψi к действительной оси. Его пропорция на
ось действительных чисел I`m, на ось мнимых чисел I``m.
-комплексное мгновенное значение
-комплексное действующее значение силы тока.
-комплексное действующее значение напряжения.
2.3 Цепь переменного тока с резистором. Векторная диаграмма. Закон Ома в комплексной форме.
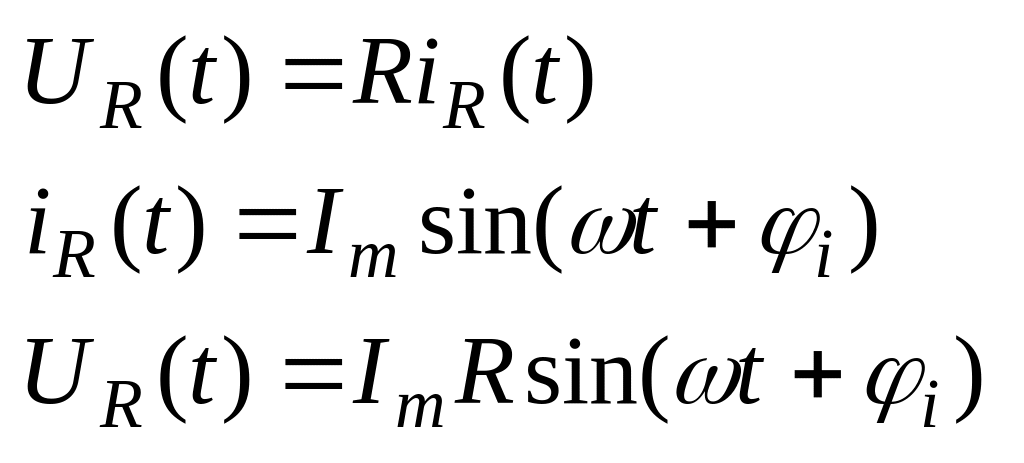
Напряжение на резисторе всегда совпадают
Комплексное сопротивление резистивного элемента.
Комплексным сопротивлением элемента наз отношения комплекса падения напряжения на элементе к комплексу тока, протекающего ч/з элемент.
Z - комплексное сопротивление
Векторная диаграмма токов и напряжений на резистивном элементе.
Векторной диаграммой наз совокупность комплексов напряжений и токов на комплексной плоскости
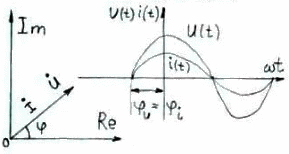
З. Ома в комплексной форме
I=U/(R+j(XL-Xc))