Равнопеременное движение материальной точки по окружности
При равнопеременном движении по окружности
– модуль скорости изменяется на равную
величину за любые равные интервалы
времени (
t 
0);
– направление скорости изменяется ( n 0);
– полное ускорение формула 12) в этом движении (см. рис. 19) равно
= n + t ,
,
где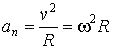 
;
Угловое ускорение – это физическая величина равная отношению изменения угловой скорости к интервалу времени, за который оно произошло.
– угловое ускорение 
в
этом движении – величина постоянная,
так как 
w =
const:
ср = мгн = const.
; 
.
(45)
Если вращение около закрепленной оси
(рис. 36), то направления векторов углового
ускорения и угловой скорости совпадают 
при
равноускоренном вращении (w > w0)
и противоположны 
при
равнозамедленном вращении (w < w0).
Таким образом, направления
векторов
и 
аналогичны
направлениям векторов
и 
.
Соотношения между
и
аналогичны соотношениям между
и
.
Формула мгновенной угловой скорости, как следует из формулы , равна:
.
– формула модуля угловой скорости:
.
– формула углового пути при равнопеременном движении точки по окружности:
.
(47)
.
Еще одну формулу углового пути можно
получить, подставив в формулу (47)
значения 
и
интервала времени 
(из
формулы (46)):
.
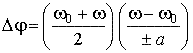
Итак, угловой путь, угловая скорость и угловое ускорение связаны между собой так же, как и соответствующие им линейные величины S, v и a.
– Уравнение равнопеременного движения материальной точки по окружности. Из формулы следует, что
.
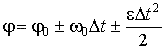Типы взаимодействия в механике. Особенности проявления
Гравитационное взаимодействие
В
рамках классической
механики гравитационное
взаимодействие описывается законом
всемирного тяготения Ньютона,
который гласит, что сила гравитационного
притяжения между двумя материальными
точками массы 
и 
,
разделёнными расстоянием 
,
пропорциональна обеим массам и обратно
пропорциональна квадрату расстояния —
то есть:
Здесь 
— гравитационная
постоянная,
равная примерно 6,6725×10−11 м³/(кг·с²).
Закон справедлив для:
1. Однородных шаров.
2. Для материальных точек.
3. Для концентрических тел.
Гравитационное взаимодействие существенно при больших массах.
Сила направлена вдоль прямой, соединяющей тела.
Пусть m1=m2=1 кг, R=1 м, тогда: G=F (численно).
Физический смысл гравитационной постоянной:
гравитационная постоянная численно равна модулю силы тяготения, действующей между двумя точечными телами массой по 1 кг каждое, находящимися на расстоянии 1 м друг от друга.
То, что гравитационная постоянная G очень мала показывает, что интенсивность гравитационного взаимодействия мала.
Сила тяжести - это сила притяжения тел к Земле (к планете).
-
из закона Всемирного тяготения. (где M -
масса планеты, m -
масса тела, R -
расстояние до центра планеты).
-
сила тяжести из второго закона Ньютона
(где m -
масса тела, g -
ускорение силы тяжести).
|
|
Если
обозначить R0 радиус
планеты, а h -
расстояние до тела от поверхности
планеты, то: |
|
Ускорение силы тяжести зависит: 1. Массы планеты. 2. Радиуса планеты. 3. От высоты над поверхностью планеты. 4. От географической широты (на полюсах - 9,83 м/с2. на экваторе - 9,79 м/с2. 5. От залежей полезных ископаемых. Упругое взаимодействие Природа упругого взаимодействия – межмолекулярное взаимодействие (притяжение и отталкивание) Типы деформации: А) в зависимости от направления воздействия - растяжение, сжатие - сдвиг - кручение В случае кручения комбинированная деформация (растяжение-сжатие и сдвиг) Б) По характеру реакции деформируемого образца -упругие - пластичные Деформация называется упругой, если она исчезает после удаления вызвавшей её нагрузки, и пластической, если после снятия нагрузки она не исчезает (во всяком случае, полностью). Закон Гука Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации Для тонкого растяжимого стержня закон Гука имеет вид:
Здесь Коэффициент
упругости зависит как от свойств
материала, так и от размеров стержня.
Можно выделить зависимость от размеров
стержня (площади поперечного сечения
Величина Если ввести относительное удлинение
и нормальное напряжение в поперечном сечении
то закон Гука в относительных единицах запишется как
В такой форме он справедлив для любых малых объёмов материала. Трение (сухое) – твердого тела по поверхности твердого тела Сила трения - это сила, возникающая в месте соприкосновения тел и препятствующая их относительному движению. Причины возникновения силы трения: 1) Шероховатость соприкасающихся поверхностей. 2)Взаимное притяжение молекул этих поверхностей. 3) Зависит от того, насколько сильно мы их прижимаем друг к другу (их взаимодействие). Сила трения прямо пропорциональна весу тела (P) и силе нормальной реакции (N). Вывод: чем больше вес тела, тем больше сила трения. Виды При наличии относительного движения двух контактирующих тел силы трения, возникающие при их взаимодействии, можно подразделить на:
В физике взаимодействия трение принято разделять на:
Закон Амонтона — Кулона
Основной характеристикой трения
является коэффициент трения
В простейших случаях сила трения
и
нормальная нагрузка (или
сила нормальной реакции)
обращающимся в равенство только при наличии относительного движения. Это соотношение называется законом Амонтона — Кулона.
Явление инерции – тела стремятся сохранить свои скорости неизменными. Масса тела характеризует инертные свойства данного тела. И́мпульс (Количество движения) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:
1 закон Ньютона Существуют такие системы отсчета, в которых тело остается неподвижным или равномерно и прямолинейно движется, если на него не действуют другие тела или действия других тел скомпенсировано. Системы отсчета: -Инерциальные СО Задается первым законом Ньютона. Идеальные СО. Землю можно рассматривать, как ИСО, если не учитывать ее вращения Время процесса <<Время обращения Земли - Неинерциальные СО СО, которые двигаются с ускорением относительно ИСО
2 закон Ньютона Ускорение тела пропорционально силе характеризующей внешнее действие на тело и обратно пропорционально массе данного тела
В инерциальной системе отсчета производная импульса материальной точки по времени равна действующей на него силе[2].
где
При́нцип суперпози́ции - результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил. 3 закон Ньютона При механическом взаимодействии тела действуют друг на друга с силами равными по величине, но противоположными по направлению.
|
|
-
ускорение силы тяжести не зависит от
массы тела (опыты Галилея).
—
сила, которой растягивают (сжимают)
стержень, 
—
абсолютное удлинение (сжатие) стержня,
а 
— коэффициент
упругости (или жёсткости).
и
длины 
)
явно, записав коэффициент упругости
как
называется модулем
упругости первого рода или модулем
Юнга и является механической
характеристикой материала.
,
который определяется материалами, из
которых изготовлены поверхности
взаимодействующих тел.
связаны
неравенством
.
— импульс (количество
движения) тела, 
— время,
а 
— производная по
времени.
Границы применимости законов:
Размеры тела д.б. существенно большими элементарных частиц
Скорость движения тела д.б. существенно меньше скорости света (чтобы не учитывать релятивистский эффект)