
Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования
«Финансовый университет
При правительстве российской федерации»
(Финансовый университет)
Кафедра «статистика»
Лабораторная работа
По статистике
Вариант 8.
Выполнил:
студент Логинов А.Б.
группы 113мфм2-01
Проверил:
Медведев В.Г.
Москва 2012
Часть А. «Сводка и группировка статистических материалов»
Отсортируем данные по факторному признаку - объем производства продукции № 2, тыс.шт. Результативным признаком будет являться рентабельность, %. Сгруппируем эти данные исходя из формулы Стерджесса, определяющей оптимальное количество групп и формулы, определяющей величину интервала.
![]() (≈3),
где n –
число получившихся групп, N
– количество единиц в совокупности.
(≈3),
где n –
число получившихся групп, N
– количество единиц в совокупности.
![]()
![]()
В соответствии с этим расчетом, выделим следующие группы:
«1-2,3», «2,3-3,6», «3,6-4,9»
Представим группировку в Табл.1
Р
Табл.1
№ группы |
Группы предприятий по объем производства продукции № 2, тыс.шт. |
№ предприятия |
объем производства продукции № 2, тыс.шт. (x) |
рентабельность, % (f) |
Количество предприятий в группе |
1 |
"1-2,3" |
3 |
1 |
13,7 |
1 |
1 |
1,1 |
12,5 |
1 |
||
2 |
1,4 |
12,9 |
1 |
||
4 |
1,7 |
14,2 |
1 |
||
5 |
1,9 |
15,9 |
1 |
||
6 |
1,9 |
15,4 |
1 |
||
7 |
2,1 |
16 |
1 |
||
8 |
2,3 |
15,9 |
1 |
||
Итого по группе 1 |
13,4 |
100,6 |
8 |
||
2 |
"2,3-3,6" |
10 |
2,7 |
16,1 |
1 |
9 |
2,9 |
16 |
1 |
||
13 |
2,9 |
22,1 |
1 |
||
11 |
3 |
18,4 |
1 |
||
12 |
3,1 |
23,4 |
1 |
||
14 |
3,3 |
25 |
1 |
||
Итого по группе 2 |
17,9 |
121 |
6 |
||
3 |
"3,6-4,9" |
15 |
3,7 |
26,8 |
1 |
16 |
3,7 |
28,6 |
1 |
||
17 |
3,8 |
22 |
1 |
||
19 |
3,8 |
23,1 |
1 |
||
18 |
3,9 |
22,6 |
1 |
||
20 |
4 |
23,8 |
1 |
||
21 |
4,4 |
24,4 |
1 |
||
22 |
4,6 |
25,1 |
1 |
||
23 |
4,7 |
25,6 |
1 |
||
24 |
4,9 |
26,2 |
1 |
||
Итого по группе 3 |
41,5 |
248,2 |
10 |
||
Итого по совокупности |
72,8 |
469,8 |
24 |
||
Построим интервальный вариационный ряд распределения по данным таблицы 1.
В
Табл.2
Р
Табл.2
объем производства продукции № 2, тыс.шт. |
число предприятий |
объем производства продукции № 2, тыс.шт. |
рентабельность, % |
средняя рентабельность в расчете на 1 предприятие, % |
1-2,3 |
8 |
13,4 |
100,6 |
12,58 |
2,3-3,6 |
6 |
17,9 |
121 |
20,17 |
3,6-4,9 |
10 |
41,5 |
248,2 |
24,82 |
ИТОГО |
24 |
72,8 |
469,8 |
19,575 |
Анализ данных таблицы 2 позволяет сделать следующие выводы:
На 24 предприятиях объем производства продукции № 2 составил 72,8 тыс.шт., рентабельность – 469,8%
В первую группу вошли 8 предприятий, на которых объем производства продукции № 2 составил 13,4 тыс.шт., рентабельность – 100,6%, а средняя рентабельность в расчете на 1 предприятие – 12,58%
Во вторую группу вошли 6 предприятий, на которых объем производства продукции № 2 составил 17,9 тыс.шт. , рентабельность – 121%, а средняя рентабельность в расчете на 1 предприятие – 20,17%
В третью группу вошли 10 предприятий, на которых объем производства продукции № 2 составил 41,5 тыс шт. , рентабельность – 248,2%, а средняя рентабельность в расчете на 1 предприятие – 24,82%
Ч
Табл.3
Вспомагательная таблица для рассчетов
|
объем производства продукции № 2, тыс.шт. (x) |
кол-во предприятий (f) |
Накопленные частоты, S |
/Х-Хср/ |
(Х-Хср)^2 |
1 |
1 |
1 |
1,52 |
2,3104 |
|
1,1 |
1 |
2 |
1,42 |
2,0164 |
|
1,4 |
1 |
3 |
1,12 |
1,2544 |
|
1,7 |
1 |
4 |
0,82 |
0,6724 |
|
1,9 |
2 |
6 |
0,62 |
0,3844 |
|
2,1 |
1 |
7 |
0,42 |
0,1764 |
|
2,3 |
1 |
8 |
0,22 |
0,0484 |
|
2,7 |
1 |
9 |
0,18 |
0,0324 |
|
2,9 |
2 |
11 |
0,38 |
0,1444 |
|
3 |
1 |
12 |
0,48 |
0,2304 |
|
3,1 |
1 |
13 |
0,58 |
0,3364 |
|
3,3 |
1 |
14 |
0,78 |
0,6084 |
|
3,7 |
2 |
16 |
1,18 |
1,3924 |
|
3,8 |
2 |
18 |
1,28 |
1,6384 |
|
3,9 |
1 |
19 |
1,38 |
1,9044 |
|
4 |
1 |
20 |
1,48 |
2,1904 |
|
4,4 |
1 |
21 |
1,88 |
3,5344 |
|
4,6 |
1 |
22 |
2,08 |
4,3264 |
|
4,7 |
1 |
23 |
2,18 |
4,7524 |
|
4,9 |
1 |
24 |
2,38 |
5,6644 |
|
ИТОГ |
60,5 |
24 |
|
22,38 |
33,618 |
По результативному признаку (расчет ведется по таблице3):
Модальное значение
 2,
X соотв=1,9;
2,9; 3,8, следовательно моды нет.
2,
X соотв=1,9;
2,9; 3,8, следовательно моды нет.
Вывод: наиболее повторяющегося значения нет
Медианное значение
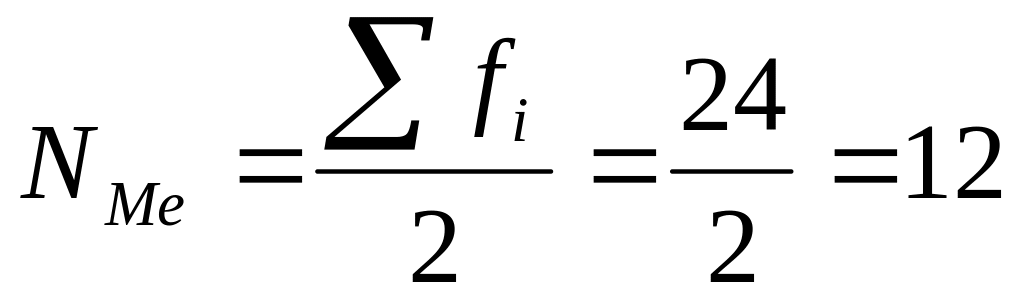 ,
,
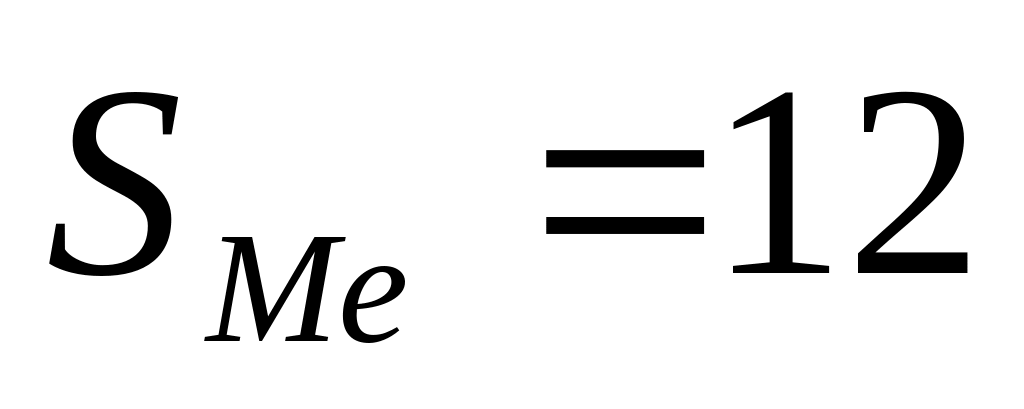 ,
Xсоотв=3,
следовательно Ме=3.
,
Xсоотв=3,
следовательно Ме=3.
Вывод: 50% предприятий произвели продукции № 2 не более 3 тыс.шт. каждое
Квартили
![]() :
:
![]() ,
,
![]() ,
Xсоотв=1,9,
следовательно
=1,9
,
Xсоотв=1,9,
следовательно
=1,9
Вывод: 25% предприятий произвели продукции № 2 не более 1,9 тыс.шт. каждое
![]() :
:
![]() ,
,
![]() Xсоотв=3,8,
следовательно
=3,8
Xсоотв=3,8,
следовательно
=3,8
Вывод: 75% предприятий произвели продукции № 2 не более 3,8 тыс.шт. каждое
![]() =
Ме=3
=
Ме=3
Децили
![]()
![]() :
:
![]() ,
,![]() ,
Xсоотв=1,4,
следовательно
=1,4
,
Xсоотв=1,4,
следовательно
=1,4
Вывод: 10% предприятий произвели продукции № 2 не более 1,4 тыс.шт. каждое
![]() :
:
![]() ,
,![]() ,
Xсоотв=1,9,
следовательно
=1,9
,
Xсоотв=1,9,
следовательно
=1,9
Вывод: 20% предприятий произвели продукции № 2 не более 1,9 тыс.шт. каждое
![]() :
:
![]() ,
,![]() ,
Xсоотв=2,3,
следовательно
=2,3
,
Xсоотв=2,3,
следовательно
=2,3
Вывод: 30% предприятий произвели продукции № 2 не более 2,3 тыс.шт. каждое
![]() :
:
![]() ,
,![]() ,
Xсоотв=2,9,
следовательно
=2,9
,
Xсоотв=2,9,
следовательно
=2,9
Вывод: 40% предприятий произвели продукции № 2 не более 2,9 тыс.шт. каждое
![]() :
:
![]() ,
,![]() ,
Xсоотв=3,7,
следовательно
=3,7
,
Xсоотв=3,7,
следовательно
=3,7
Вывод: 60% предприятий произвели продукции № 2 не более 3,7 тыс.шт. каждое
![]() :
:
![]() ,
,![]() ,
Xсоотв=3,8,
следовательно
=3,8
,
Xсоотв=3,8,
следовательно
=3,8
Вывод: 70% предприятий произвели продукции № 2 не более 3,8 тыс.шт. каждое
![]() :
:
![]() ,
,![]() ,
Xсоотв=4,
следовательно
=4
,
Xсоотв=4,
следовательно
=4
Вывод: 80% предприятий произвели продукции № 2 не более 4 тыс.шт. каждое
![]() :
:
![]() ,
,![]() ,
Xсоотв=4,6,
следовательно
=4,6
,
Xсоотв=4,6,
следовательно
=4,6
Вывод: 90% предприятий произвели продукции № 2 не более 4,6 тыс.шт. каждое
![]() =Ме=3
=Ме=3
объем производства продукции № 2, тыс.шт. |
число предприятий |
объем производства продукции № 2, тыс.шт. |
рентабельность, % |
средняя рентабельность в расчете на 1 предприятие, % |
Н
Табл.4 |
1-2,3 |
8 |
13,4 |
100,6 |
12,58 |
8 |
2,3-3,6 |
6 |
17,9 |
121 |
20,17 |
14 |
3,6-4,9 |
10 |
41,5 |
248,2 |
24,82 |
24 |
ИТОГО |
45 |
72,8 |
469,8 |
19,575 |
|
По полученной в Части А (пункт 1) группировке по первому факторному показателю (расчет ведется по таблице4):
Мода: модальный интервал –« 3,6-4,9»
![]() тыс.шт,т.е.
в данной совокупности больше всего
организаций с объемом производства
6,24
тыс.шт,т.е.
в данной совокупности больше всего
организаций с объемом производства
6,24
Медиана:
,
![]() ,
соотв. интервал – «2,3-3,6»
,
соотв. интервал – «2,3-3,6»
 т.е.
половина организаций в совокупности
произвела не более 3,97 тыс.шт.
т.е.
половина организаций в совокупности
произвела не более 3,97 тыс.шт.
По результативному показателю и факторным показателям рассчитаем и проанализируем (расчет ведется по таблице3):
Среднее значение
![]()
 4,9-1=3,9
– пределы колеблемости признака в
совокупности.
4,9-1=3,9
– пределы колеблемости признака в
совокупности.
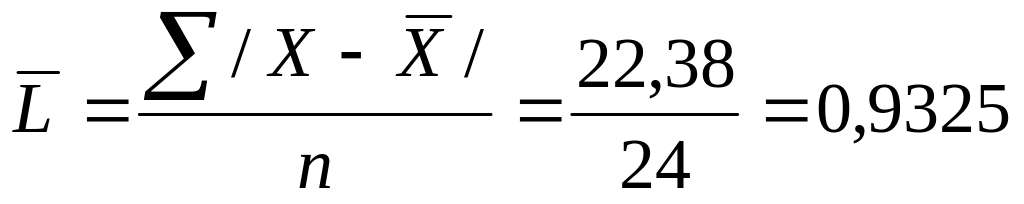
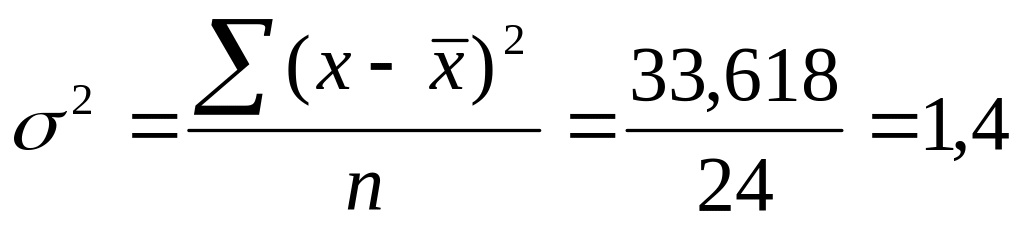

 ,
т.е. колеблемость крайних значений
признака вокруг средней составляет
154,8%
,
т.е. колеблемость крайних значений
признака вокруг средней составляет
154,8% ,
т.е. доля усреднённого значения абсолютных
отклонений от средней величины составляет
37%
,
т.е. доля усреднённого значения абсолютных
отклонений от средней величины составляет
37% ,
т.е. совокупность недостаточно однородна
по изучаемому признаку, а средняя
недостаточно типична, т.к. 30%≤
,
т.е. совокупность недостаточно однородна
по изучаемому признаку, а средняя
недостаточно типична, т.к. 30%≤ ≤60%
≤60%
Часть D. «Статистическое изучение взаимосвязей финансово-экономических показателей»
Построим корреляционное поле результативного показателя с факторным показателем – объем производства товара №2 по данным таблицы5
y
Рисунок позволяет сделать вывод о наличии сильной линейной статистической связи между показателями x и y. При этом связь имеет положительную тенденцию, т.е. с ростом переменной X наблюдается увеличение Y.
2) Рассчитаем коэффициенты корреляции Фехнера и Спирмена, взяв в качестве факторного признака объем производства продукции № 2 (расчеты велись по таблице5)
Коэффициент знаков Фехнера:
Отр – отрицательное число
Пол – положительное число
Xср=2,52
Yср=20,24
![]() ,
где u –
Rчисло
совпадений, v
– число несовпадений
,
где u –
Rчисло
совпадений, v
– число несовпадений
u = 21
v = 3
![]() -
прослеживается прямая и тесная связь
показателей
-
прослеживается прямая и тесная связь
показателей
Коэффициент рангов Спирмена:
![]()
![]()
![]()
![]() -
связь тесная и прямая
-
связь тесная и прямая
x |
y |
X-Xср |
Y-Yср |
Rx |
Ry |
d
Табл.5 |
1 |
13,7 |
отр |
отр |
1 |
3 |
4 |
1,1 |
12,5 |
отр |
отр |
2 |
1 |
1 |
1,4 |
12,9 |
отр |
отр |
3 |
2 |
1 |
1,7 |
14,2 |
отр |
отр |
4 |
4 |
0 |
1,9 |
15,9 |
отр |
отр |
5,5 |
6,5 |
1 |
1,9 |
15,4 |
отр |
отр |
5,5 |
5 |
0,25 |
2,1 |
16 |
отр |
отр |
7 |
8 |
1 |
2,3 |
15,9 |
пол |
отр |
8 |
6,5 |
2,25 |
2,7 |
16,1 |
пол |
отр |
9 |
10 |
1 |
2,9 |
16 |
пол |
отр |
10,5 |
9 |
2,25 |
2,9 |
22,1 |
пол |
пол |
10,5 |
13 |
6,25 |
3 |
18,4 |
пол |
пол |
12 |
11 |
1 |
3,1 |
23,4 |
пол |
пол |
13 |
16 |
9 |
3,3 |
25 |
пол |
пол |
14 |
19 |
25 |
3,7 |
26,8 |
пол |
пол |
15,5 |
23 |
56,25 |
3,7 |
28,6 |
пол |
пол |
15,5 |
24 |
72,25 |
3,8 |
22 |
пол |
пол |
17,5 |
12 |
30,25 |
3,8 |
23,1 |
пол |
пол |
17,5 |
15 |
6,25 |
3,9 |
22,6 |
пол |
пол |
19 |
14 |
25 |
4 |
23,8 |
пол |
пол |
20 |
17 |
9 |
4,4 |
24,4 |
пол |
пол |
21 |
18 |
9 |
4,6 |
25,1 |
пол |
пол |
22 |
20 |
4 |
4,7 |
25,6 |
пол |
пол |
23 |
21 |
4 |
4,9 |
26,2 |
пол |
пол |
24 |
22 |
4 |
5) Построим уравнение линейной регрессии
![]() -
уравнение линейной регрессии, обозначив
за х – объем производства товара№2, а
за y
–рентабельноть, n=45.
-
уравнение линейной регрессии, обозначив
за х – объем производства товара№2, а
за y
–рентабельноть, n=45.
Чтобы
составить уравнение линейной регрессии,
решим следующую систему, найдем
![]() и
и
![]() .
.
![]()
![]()
Для расчетов понадобится таблица 6.
x |
y |
x^2 |
xy |
Табл.6 |
1 |
13,7 |
1 |
13,7 |
|
1,1 |
12,5 |
1,21 |
13,75 |
|
1,4 |
12,9 |
1,96 |
18,06 |
|
1,7 |
14,2 |
2,89 |
24,14 |
|
1,9 |
15,9 |
3,61 |
30,21 |
|
1,9 |
15,4 |
3,61 |
29,26 |
|
2,1 |
16 |
4,41 |
33,6 |
|
2,3 |
15,9 |
5,29 |
36,57 |
|
2,7 |
16,1 |
7,29 |
43,47 |
|
2,9 |
16 |
8,41 |
46,4 |
|
2,9 |
22,1 |
8,41 |
64,09 |
|
3 |
18,4 |
9 |
55,2 |
|
3,1 |
23,4 |
9,61 |
72,54 |
|
3,3 |
25 |
10,89 |
82,5 |
|
3,7 |
26,8 |
13,69 |
99,16 |
|
3,7 |
28,6 |
13,69 |
105,82 |
|
3,8 |
22 |
14,44 |
83,6 |
|
3,8 |
23,1 |
14,44 |
87,78 |
|
3,9 |
22,6 |
15,21 |
88,14 |
|
4 |
23,8 |
16 |
95,2 |
|
4,4 |
24,4 |
19,36 |
107,36 |
|
4,6 |
25,1 |
21,16 |
115,46 |
|
4,7 |
25,6 |
22,09 |
120,32 |
|
4,9 |
26,2 |
24,01 |
128,38 |
|
72,8 |
485,7 |
251,68 |
1594,71 |
итог |
![]()
![]()
На основе решения этой системы уравнений получаем:
а
- параметры уравнения линейной регрессии
a1=3,94
![]()
![]()
![]()
![]()
Выводы:
Так как a1=3,94, значение результативного признака при изменении факторного на единицу в среднем приведет к изменению в 3,94 раз.
Так как а0=8,29, усредненное влияние на результативный признак за счет неучтенных факторов будет равен 8,29
Часть Е. «Ряды динамики»
Используя данные ежегодника за 2011 год, проведем анализ динамики социально-экономических явлений, рассчитав показатели ряда динамики, такие как: цепные/базисные абсолютные приросты, цепные/базисные темпы роста, цепные/базисные темпы прироста, абсолютное значение одного процента прироста. Также вычислим средние показатели: средний абсолютный прирост, средний темп роста, средний темп прироста, средний уровень ряда.
И
Табл.7
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
17,9 |
17,5 |
18 |
18,5 |
19 |
19,1 |
19 |
Для вычислений используем следующие формулы:
Цепные абсолютные приросты:
![]() ;
;
Базисные абсолютные приросты:
![]()
(первый уровень ряда принят в качестве базисного);
Цепные темпы роста:
![]() ;
;
Базисные темпы роста:
![]()
(первый уровень ряда принят в качестве базисного) ;
Цепные темпы прироста:
![]() ;
;
Базисные темпы прироста:
;
Результаты расчетов приведены в таблице 8.
Х
Табл.8
Год |
Y |
Цепные абсолютные приросты |
Базисные абсолютные приросты |
Цепные темпы роста |
Базисные темпы роста |
Цепные темпы прироста |
Базисные темпы прироста |
2005 |
17,9 |
|
0 |
|
100 |
|
0 |
2006 |
17,5 |
-0,4 |
-0,4 |
0,97765363 |
0,9776536 |
-0,02234637 |
-0,02234637 |
2007 |
18 |
0,5 |
0,1 |
1,02857143 |
1,0055866 |
0,02857143 |
0,005586592 |
2008 |
18,5 |
1 |
0,6 |
1,02777778 |
1,0335196 |
0,02777778 |
0,033519553 |
2009 |
19 |
1,5 |
1,1 |
1,02702703 |
1,0614525 |
0,02702703 |
0,061452514 |
2010 |
19,1 |
1,6 |
1,2 |
1,00526316 |
1,0670391 |
0,00526316 |
0,067039106 |
2011 |
19 |
1,5 |
1,1 |
0,9947644 |
1,0614525 |
-0,0052356 |
0,061452514 |
Сумма |
129 |
|
|
|
|
|
|
Теперь рассчитаем средние показатели изменения уровней ряда динамики.
Средний уровень ряда
![]()
Показатели динамического ряда
Средний абсолютный прирост:
![]()
Динамика положительная
Средний темп роста:
![]()
Средний темп прироста:
![]()
Проведем аналитическое выравнивание ряда динамики по прямой для выявления тенденции изменения производства сахара песка. Для выравнивания ряда по прямой используем уравнение
![]()
параметры которого a0 и a1 на основании метода наименьших квадратов путем решения системы нормальных линейных уравнений
![]()
 ,
,
![]() .
.
Д ля
упрощения расчетов показателям времени
t
придадим такие значения, чтобы их сумма
была равна нулю. В
этом случаем системы уравнений принимает
вид
ля
упрощения расчетов показателям времени
t
придадим такие значения, чтобы их сумма
была равна нулю. В
этом случаем системы уравнений принимает
вид
![]()
![]()
Отсюда:
![]() ,
,
![]() .
.
Ч
Табл. 9
Виды акций |
Среднегодовая цена акции, тыс. руб. |
Продано, млн. шт. |
объемов торгов, тыс.руб. |
|||
2006 г. (po) |
2008 г. (p1) |
2006 г. (qo) |
2008 г. (q1) |
2006 г. (po*q0) |
2008 г. (p1*q1) |
|
Б |
15,7 |
16,5 |
1,7 |
1,8 |
26,69 |
29,7 |
В |
20,7 |
21,3 |
2,9 |
2,9 |
60,03 |
61,77 |
Д |
23,6 |
23,9 |
1,7 |
1,6 |
40,12 |
38,24 |
Рассчитаем индивидуальные и общие индексы: цен, физического объема продаж, объемов торгов в рублевом выражении.
Индивидуальные индексы по видам акций Б:
![]() 1,05
или 105%
1,05
или 105%
![]() 1,059
или 105,9%
1,059
или 105,9%
![]() 1,113
или 111,3%
1,113
или 111,3%
Индивидуальные индексы по видам акций В:
![]() 1,029
или 102,9 %
1,029
или 102,9 %
![]() 1
или 100%
1
или 100%
![]() 1,029
или 102,9%
1,029
или 102,9%
Индивидуальные индексы по видам акций Д:
![]() 1,013
или 101,3%
1,013
или 101,3%
![]() 0,941
или 94,1%
0,941
или 94,1%
![]() 0,953
или 95,3%
0,953
или 95,3%![]()
Общие индексы:
![]() или
102,9%
или
102,9%
![]() 0,997
или 99,7%
0,997
или 99,7%
![]() 1,023
или 102,3%
1,023
или 102,3%
Абсолютное изменение объемов торгов в рублевом выражении: общее, за счет изменения цен, за счет изменения физического объема продаж.
![]()
![]()
![]()
Средневзвешенную цену акций за указанные периоды.
![]() =20,13
тыс.руб.
=20,13
тыс.руб.
![]() 20,6
тыс.руб.
20,6
тыс.руб.
Абсолютное и относительное изменение средней цены акций за указанный период: общее, за счет изменения индивидуальных цен на акции; за счет изменения физического объема продаж акций.
![]()
