- •1.Общие сведения о системах связи. Описание структурной схемы. Основные понятия.
- •2 Модели непрерывных каналов связи
- •3.Характеристики системы связи
- •4. Модели дискретных каналов связи.
- •5. Матем. Модели сообщений, сигналов и помех.
- •6.Оптимальные алгоритмы когерент приема с-лов
- •7.Спектральное и временное представление периодических сигналов
- •8. Некогерентный прием сигналов
- •9. Спектральное представление непериодических сигналов и его свойства.Ширина спектра.
- •10.Оптимальная демодуляция и фильтрация непрерывных сигналов
- •12. Критерии качества и правила приема дискретных сообщений
- •13.Аналого-цифровое и цифро-аналоговое преобразование сигналов. Методы построения ацп и цап, основные параметры.
- •14.Критерии помехоустойчивости приема непрерывных сообщений.
- •Таким образом, спектр простого ам сигнала содержит несущее и два боковых колебания , где – частота модулирующего_сигнала.
- •1. Спектр ам сигнала содержит:
- •2. Ширина спектра ам сигнала вдвое больше максимальной модулирующей частоты
- •16. Преобразование детерм. И случ. Сигналов в линейных цепях.
- •3.Мост Вина
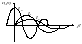
- •Детектирование чм сигналов
- •18.Пропускная способность многоканальных систем связи.
- •21. Сигналы дискретной модуляции аМн, чМн, фМн, их спектральное представление.
- •22 Безопасность информации. Виды умышленных угроз
- •23.Формирование и детектирование сигналов с импульсной модуляцией.
- •24.Криптографические методы защиты информации (симметричные криптосистемы).
- •25.Криптографические методы защиты информации (асимметричные криптосистемы).
- •26.Основные характеристики случайных процессов. Акф, вкф и их свойства.
- •27.Методы и средства защиты данных в телекоммуникационныъх сетях
- •28.Спектральный анализ случайных процессов.
- •29.Методы повышения эф-ти сс.
- •31.Потенциальная верность приема сообщений при различных видах модуляции.
- •32.Основы теории разделения сигналов в многоканальных системах. Частотное уплотнение.
- •33.Цифровые методы передачи непрерывных сообщений.
- •34.Основы теории разделения сигналов в многоканальных системах. Временное уплотнение.
- •36.Основы теории разделения сигналов в многоканальных системах. Комбинационное и кодовое уплотнение.
- •37.Элементы цифровой обработки сигналов. Цифровые фильтры.
- •Рекурсивный фильтр (рцф)
- •Нерекурсивный фильтр (нцф)
- •38.Квантовая криптография.
- •39.Принципы построения защищенных ткс.
- •40.Хаотические системы связи.
16. Преобразование детерм. И случ. Сигналов в линейных цепях.
1.ФНЧ
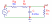
– это схема, передающая без значительных изменений сигналы нижних частот, а на высоких частотах выходной сигнал меньше входного по амплитуде и запаздывает по фазе относительно входных сигналов. Наиболее сильно интегрирующие свойства проявляются на частотах f>fср. При импульсном воздействии на заданной частоте ФНЧ ведет себя как интегрирующая цепь. При понижении частоты форма выходного сигнала приближается к форме входного; при увеличении – коэффициент усиления понижается, поэтому фильтр не пропускает высокие частоты. Реализация ФНЧ может быть разнообразной, включая электронные схемы, программные алгоритмы, акустические барьеры, механические системы и т.д. Например, электронные фильтры нижних частот используются для подавления пульсаций напряжения на выходе выпрямителей переменного тока, для разделения частотных полос в акустических системах, в системах передачи данных для подавления высокочастотных помех и ограничения спектра сигнала. Также, радиопередатчики используют низкочастотные фильтры для блокировки гармонических излучений, которые могут взаимодействовать с низкочастотным полезным сигналом и создавать помехи другим радиоэлектронным средствам и т.д.
2.ФВЧ
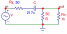
– схема, передающая без изменений сигналы высоких частот, а на низких частотах обеспечивает затухание сигналов и опережение их по фазе относительно входных сигналов. При импульсном воздействии заданной частоты ФВЧ ведёт себя как дифференцирующая цепь. При повышении частоты форма выходного сигнала приближается к форме входного; при понижении длительность импульсов сильно укорачивается. Применение: часто используется в обработке аудио сигналов. Ещё одно важное применение ФВЧ - устранение постоянной составляющей сигнала, для чего частоту среза выбирают очень низкой. Также используются в обработке изображений (для определения границ).
3.Мост Вина
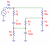
представляет собой последовательно соединённые ФНЧ и ФВЧ, дополненные омическим делителем. АЧХ на fср имеет минимум. Режекторный фильтр – фильтр, имеющий полосу задержания, расположеную между двумя полосами пропускания. Такой фильтр позволяет подавлять сильные гармонические помехи, вырезая из спектра полезного сигнала сравнительно узкую полосу частот и пропуская все остальные составляющие спектра без ослабления На частоте среза сдвиг фаз меняется на противоположный (на 180о). Погрешность не превысила 2% (получилась 0,08%). Применение: для построения автогенераторов, обладающих удовлетворительной стабильностью и диапазоном генерируемых частот, иногда применяется в кач-ве фильтра. Автогенератор на основе моста Вина – в сущности операционный усилитель, охваченный частотно-зависимой положительной обратной связью.
17.ЧМ – сигналы, их временное и спектральное представление. Детектирование ЧМ – сигналов.
2. ЧМ - сигналы, спектральный анализ
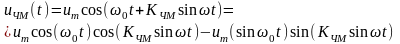
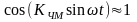
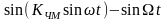
при
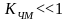
Из выражения следует, что спектр ЧМ – сигнала, при малом коэффициенте модуляции ( ), повторяет спектр АМ – сигнала.
 ,
,
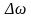 - девиация частоты
- девиация частоты
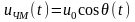
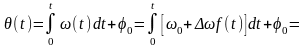
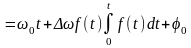
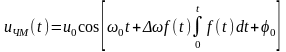 - общий случай
- общий случай
Для
того чтобы получить спектр ЧМ – сигнала,
вернемся к частному случаю
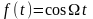

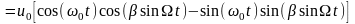
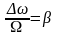 - индекс ЧМ
- индекс ЧМ
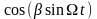 и
и
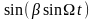 - разложение по системе Бесселевых
функций
- разложение по системе Бесселевых
функций
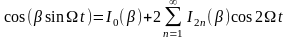
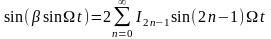
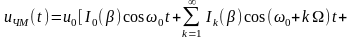
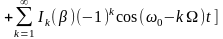
Для
величины
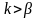 амплитуды составляющих спектра
становиться настолько малыми, что ими
можно пренебречь, поэтому ширина спектра
ЧМ – сигнала может быть ограничена той
полосой частот, в пределах которых
амплитуды составляющих
амплитуды составляющих спектра
становиться настолько малыми, что ими
можно пренебречь, поэтому ширина спектра
ЧМ – сигнала может быть ограничена той
полосой частот, в пределах которых
амплитуды составляющих
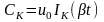 превышают
превышают
 на
на
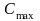 ,
где
- наибольшее значение амплитуды боковой
частоты,
выбирается в пределах -
,
где
- наибольшее значение амплитуды боковой
частоты,
выбирается в пределах -
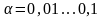
Определяется,
таким образом, полоса частот называемая
действительной шириной спектра ЧМ –
сигнала, обозначается -
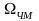 .
.
Пусть
n
– число
спектральных линий в каждой боковой
полосе, а коэффициент
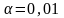 .
Тогда интервалы между спектральными
линиями будут определяться частотой
.
Тогда интервалы между спектральными
линиями будут определяться частотой
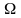
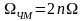
Если
теперь с помощью Бесселевых функций
для заданного
найти n,
то получиться зависимость
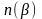

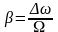 - индекс модуляции
- индекс модуляции
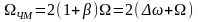
1)
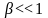 ,
,
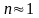 - каждая боковая полоса состоит из одной
линии
- каждая боковая полоса состоит из одной
линии
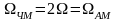 - узкополостная
ЧМ
- узкополостная
ЧМ
2)
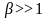 ,
,
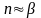
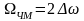
Ширина спектра не зависит от спектра модулирующей функции и равна удвоенной девиации частоты, это означает, что ЧМ широкополостная (помехоустойчивость).
Чем
выше
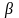 ,
тем лучше помехоустойчивость.
,
тем лучше помехоустойчивость.