4. Модели дискретных каналов связи.

Внутри ДКС всегда содержится непрерывный канал. Преобразование непрерывного в дискретный осущ-ет модем.

Простая модель: UвхДКСUвых.

Данная модель содержит множество вх и вых сигналов. Множ-во всех сигналов опис-ся распр-ем условных ввер-й.

Как вх так и вых сигнал явл-ся послед-ми . n-код символов, m-основание, T-длит передачи симв. При Т одинаковом, V=1/T кол-во символов в ед вр.

В общем случае для любых n должна быть указана вероятность того , что при подаче на вх канала заданной посл-ти кодовых импульсов B[n].

Все посл-ти, число которых равно m^n образуют n-мерное конечное вект пространство .Вектор ошибок (Е[n]) = поразрядная разность по модулю м\у переданным и принятым вектором. Это означает что прох-е дискр сигнала можно рассматривать как сложение входного вектора и вектора ошибок.

Вектор ошибок – помеха в непрерывном канале связи

Наиболее простой- двоичный(0-нет Ош, 1- есть ошибка).

1) Симметричный канал без памяти. В этом канале каждый пере­данный кодовый символ может быть принят ошибочно с вероятностью р и правильно с вероятностью 1 - р, причем в случае ошибки вместо переданного символа b может быть с равной вероятностью принят любой другой символ. Таким образом, вероятность того, что

принят символ **, если был передан ***

Термин "без памяти" означает, что вероятность ошибочного прие­ма символа не зависит от того, какие символы передавались до него и как они были приняты. Эта модель применяется тогда, когда в непрерывном канале отсутствуют замирания, а аддитивный шум белый (или квазибелый). Вероятности переходов в двоичном симметричном канале (m=2) схематически показаны в виде графа на рисунке 8.3.

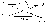
2) Симметричный канал без памяти со стиранием отличается от предыдущего тем, что алфавит на выходе канала содержит дополнительный (m+1)-й символ, обозначаемый знаком "?". Этот символ появляется тогда, когда демодулятор не может надежно опознать пе­реданный символ. Вероятность такого отказа от решения или стирания символа p_c в данной модели постоянна и не зависят от передаваемого символа. За счет введения стирания удается значительно снизить вероятность ошибки, иногда ее даже считают равной нул.. На рисунке 8.4 показаны вероятности переходов в такой модели.

3)_Несимметричный канал без памяти характеризуется, как и предыдущие модели, тем, что ошибки возникают в нем независимо друг от друга, однако вероятности ошибок зависят от того, такой символ передается. Так, в двоичном несимметричном канале вероят­ность р(1/0) приема символа 1 при передаче символа 0 не равна вероятности р (0/1) приема 0 при передаче I (рис.8.5).

Существуют и дискретные каналы с памятью, в которых вероятность ошибки зависит от того, правильно или ошибочно принята предыдущие символы.

5. Матем. Модели сообщений, сигналов и помех.

Сигналы подразделяются на: - детерм. и случ. Детерминир. сигнал – колебание, описыв. детерм. функцией времени U(t). Это означает, что любому моменту времени ti соответствует вполне определенное значение ф-ции U(t). Такие колебания никакой информации не несут, т.к. о них все известно заранее. К случайным относятся колебания, мгновенные значения которых не могут быть точно определены, а предугаданы с определенной вероятностью p<1. Детерминированные подразделяются на периодические и непериодические.

Электрические сигналы, могут быть:

- непрер по вр, непр по уровню 1 (аналоговый сигнал)

- непрер по вр, дискр по уровню 2

- дискр по вр, непрер по уровню 3

- дискр по вр, дискр по уровню 4 (цифровой сигнал)

1 2 3

4

Помехи: 1)аддитивные –склад-ся с получ. сигналом ‘S’=S(t)+n(t) 2)флуктуацион - обусловлены случайными отклонениями тех или иных физ. величин от своих ср. значений. Равномер спектральная плот-ть мощности в широкой Δf (белый шум), нулевое мат ожид-е и норм распр-е.3)импульсные – случайная посл-ть импульсов, следующих столь редко, что реакция приемника на текущий импульс успевает затухнуть (атмосферная помеха).4)узкопол – ~, спектр пл-ть кот. занимает сравнительно узкую Δf, по сравнению с сигналом 5)мультипликатив. – проявл только при пер-че сигналов и её далеее закладывают в многокр усил или ослабл. сигнала ‘S’=S(t)хn(t)

Учитывая все помехи: Z(t)=k(t)S(t)+n(t).

Аддитивные -внешние, внутренние.

Внутренние (в самой аппаратуре).

Внешние по происхождению: -атмосферные (проц. в тропосфере и ионосфере. Херят ДВ и СВ диап.), -косм. (электромагн. проц. на солнце и др. косм. объ-ектах .УКВ), -индустриальные(от эл. аппаратуры), от посторонних радиостанц. и каналов (наруш. реглам. рас-пред. раб. частот, недостат. стабильн. частот, плох. фильтрац. гармоник сигн.)

Классифик. по физ природе возникн: флуктуационные (совок. разл. помех при прох. ими трактов приемн устр-в.),сосредоточенные_по_времени,сосредоточ по спектру (значит. Часть мощн. сосредот. в небольш уч-ах диап. частот). Искажения-нежелательн. изменение формы сигнала. Бывают: линейные (неравномерн. АЧХ, нелинейность ФЧХ), нелинейные (наличие нелин. элем-ов привод. к нелин. амплитуд. хар-ки канала).

Помехоустойчивость - способн. сист. противост. вредному влиянию помех на передачу.

Функциональные пространства и их базисы.

Сигналы – это, прежде всего, процессы, т.е. функции времени x(t), существующие на ограниченном интервале Т (в теории возможно Т → ∞). Их можно изобразить графически и описывать упорядоченной последовательностью значений в отдельные моменты времени t_k

В математике под пространством понимают множество объектов (любой физической природы), наделенных некоторым общим свойством.

Метрическое пространство – это множество с подходящим образом определенным расстоянием между его элементами. Само это расстояние, как и способ его определения, называют метрикой и обозначают .

Линейным пространством L над полем F называют множество элементов , называемых векторами, для которых заданы две операции –сложение элементов (векторов) и умножение векторов на элементы из поля F (называемые скалярами).

Нормированные пространства объединяют в себе геометрические (характерные для метрических пространств) и алгебраические (для линейных пространств) свойств путем введения действительного числа, характеризующего «размер» элемента в пространстве - норму вектора и обозначают .

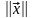Пространства со скалярным произведением

То есть с отображением упорядоченной пары векторов на поле скаляров из F. Эту операцию называют скалярным (внутренним) произведением векторов и записывают_в_вид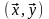е ,т.е. .