
- •1.Общие сведения о системах связи. Описание структурной схемы. Основные понятия.
- •2 Модели непрерывных каналов связи
- •3.Характеристики системы связи
- •4. Модели дискретных каналов связи.
- •5. Матем. Модели сообщений, сигналов и помех.
- •6.Оптимальные алгоритмы когерент приема с-лов
- •7.Спектральное и временное представление периодических сигналов
- •8. Некогерентный прием сигналов
- •9. Спектральное представление непериодических сигналов и его свойства.Ширина спектра.
- •10.Оптимальная демодуляция и фильтрация непрерывных сигналов
- •12. Критерии качества и правила приема дискретных сообщений
- •13.Аналого-цифровое и цифро-аналоговое преобразование сигналов. Методы построения ацп и цап, основные параметры.
- •14.Критерии помехоустойчивости приема непрерывных сообщений.
- •Таким образом, спектр простого ам сигнала содержит несущее и два боковых колебания , где – частота модулирующего_сигнала.
- •1. Спектр ам сигнала содержит:
- •2. Ширина спектра ам сигнала вдвое больше максимальной модулирующей частоты
- •16. Преобразование детерм. И случ. Сигналов в линейных цепях.
- •3.Мост Вина
- •Детектирование чм сигналов
- •18.Пропускная способность многоканальных систем связи.
- •21. Сигналы дискретной модуляции аМн, чМн, фМн, их спектральное представление.
- •22 Безопасность информации. Виды умышленных угроз
- •23.Формирование и детектирование сигналов с импульсной модуляцией.
- •24.Криптографические методы защиты информации (симметричные криптосистемы).
- •25.Криптографические методы защиты информации (асимметричные криптосистемы).
- •26.Основные характеристики случайных процессов. Акф, вкф и их свойства.
- •27.Методы и средства защиты данных в телекоммуникационныъх сетях
- •28.Спектральный анализ случайных процессов.
- •29.Методы повышения эф-ти сс.
- •31.Потенциальная верность приема сообщений при различных видах модуляции.
- •32.Основы теории разделения сигналов в многоканальных системах. Частотное уплотнение.
- •33.Цифровые методы передачи непрерывных сообщений.
- •34.Основы теории разделения сигналов в многоканальных системах. Временное уплотнение.
- •36.Основы теории разделения сигналов в многоканальных системах. Комбинационное и кодовое уплотнение.
- •37.Элементы цифровой обработки сигналов. Цифровые фильтры.
- •Рекурсивный фильтр (рцф)
- •Нерекурсивный фильтр (нцф)
- •38.Квантовая криптография.
- •39.Принципы построения защищенных ткс.
- •40.Хаотические системы связи.
26.Основные характеристики случайных процессов. Акф, вкф и их свойства.

Различают два вида случайных величин: дискретные и непрерывные. Универсальной характеристикой для них является функция распределения F1(x), определяющая вероятность того, что случайная величина x примет значение меньше некоторого числа.
F1(x)–интегральный закон распределения.
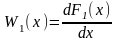 –плотность
вероятности(дифференциальный закон
распределения).
–плотность
вероятности(дифференциальный закон
распределения).
Полными вероятностными характеристиками системы случайных является законы распределения вероятности задаваемые либо F1(x), либо W1(x).
В статистической радиотехнике основное практическое значение имеют системы непрерывных случайных величин, которые характеризуются W1(x).
Наиболее важными числовыми характеристиками являются мат ожид.- mx и дисперсия- Dx и отклонение bx.
 ,
где Q1–характеристическая
функция, u–вещественная
функция.
,
где Q1–характеристическая
функция, u–вещественная
функция.
Если случайная величина изменяется во времени, то вводят понятие случайного процесса X( t).
Случайный процесс называется стационарным, если его плотность вероятности произвольного порядка n зависит только от интервала t2-t1, t3-t1…tn-t и не зависит от положения этих интервалов в области изменения аргумента t.
В радиотехнике условие стационарности ограничивается условием независимости от времени только одномерной и двумерной плотностью вероятности.
Это
позволяет считать, что mx
, Dx,
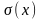 не зависят от времени, а
не зависят от времени, а
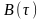 корреляционная функция не зависит от
моментов, а определяется только
.
Дальнейшее упрощение анализа достигается
при условии эргодичности процесса.
корреляционная функция не зависит от
моментов, а определяется только
.
Дальнейшее упрощение анализа достигается
при условии эргодичности процесса.
Стационарный процесс называется эргодическим если при определении любых статистических характеристик усреднение по множеству реализаций эквивалентно усреднению времени одной теоретически бесконечно длинной реализации.
АКФ
Чем
медленнее изменяется во времени
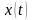 ,
тем уже энергетический спектр. С другой
стороны, скорость изменения
определяет ход корреляционной функции.
Очевидно, что между
,
тем уже энергетический спектр. С другой
стороны, скорость изменения
определяет ход корреляционной функции.
Очевидно, что между
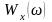 и
и
 имеется тесная связь.
имеется тесная связь.
Существует
теорема Винера — Хинчина, утверждающая,
что
и
 связаны между собой преобразованиями
Фурье;
связаны между собой преобразованиями
Фурье;


Из этих выражений вытекает свойство, аналогичное свойствам преобразований Фурье, установленным в гл. 2 для детерминированных сигналов: чем шире энергетический спектр случайного процесса, тем меньше интервал корреляции, и, соответственно, чем больше интервал корреляции, тем уже спектр процесса.
Большой
интерес представляет белый шум, когда
энергетический спектр равномерен на
всех частотах
 .
.
Если
в выражение подставить
 то получим
то получим
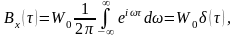
где
 — дельта-функция,
— дельта-функция,
Для
белого шума с бесконечным и равномерным
спектром корреляционная функция равна
нулю для всех значений
,
кроме
 ,
при котором
,
при котором
 обращается в бесконечность. Подобный
шум, имеющий игольчатую структуру с
бесконечно тонкими случайными выбросами,
иногда называют дельта - коррелированным
процессом. Дисперсия белого шума
бесконечно велика.
обращается в бесконечность. Подобный
шум, имеющий игольчатую структуру с
бесконечно тонкими случайными выбросами,
иногда называют дельта - коррелированным
процессом. Дисперсия белого шума
бесконечно велика.
ВКФ
Связь
между двумя стационарными процессами
и
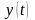 оценивается с помощью взаимно
- корреляционной
функции, определяемой выражениями
оценивается с помощью взаимно
- корреляционной
функции, определяемой выражениями

В данном параграфе рассматриваются эргодические процессы, поэтому вместо (4.46) можно применять временное усреднение


Как и для детерминированных колебаний, взаимно - корреляционная функция не изменяется, если сдвиг на одной из функций или заменить на сдвиг в обратном направлении другой функции. Поэтому можно написать следующие равенства:


Из
последних выражений вытекают следующие
соотношения между
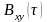 и
и
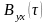 :
:

Соотношения (4.49)—(4.51) не следует смешивать с условиями четности функций. Каждая из функций и не обязательна четна относительно (см. §2.16).
В итоге корреляция между значениями функций и различных момента времени, разделенных интервалом , задается корреляционной матрицей
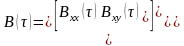
где
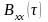 и
и
 — корреляционные функции соответственно
процессов
и
.
— корреляционные функции соответственно
процессов
и
.
