11 Дискретизация непрерывных сигналов. Теорема Котельникова

Для повышении эффективности передачи информации обычно преднамеренно ограничивают спектр передаваемых сигналов.

В телефонии диапазон частот 300-3400

Функции с ограниченным спектром обладают свойством которое подметил Котельников В.А.

Он сформулировал теорему:

Н епрерывная функция не содержащая частот выше граничной полностью определяется своими … значениями (отсчётами) в точках отстоящих друг от друга

ряд Котельникова.

Покажем, как это выглядит графически .

АЧХ идеального ФНЧ

Процедура передачи сигналов f(t) сводится

к передаче отсчётов

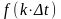
по каналу связи и восстановлению на

приёмнике по этим отсчётам ф-и f(t) путём

фильтра низких частот.

При практическом использовании этой теоремы возникают следующие трудности:

а) Для передачи сигналов отводится ограниченная полоса частот 0÷wc, хотя спектры реальных сигналов бесконечны.

f(t)- исходный сигнал. f*(t)- восстановленный с.

Если воспользоваться соотношением Парсеваля, зная

погреш.→ →

б) Реальный сигнал f(t)существует на конечном интервале наблюдений, поэтому

- частота сигнала

- врем. набл.

Максимальная величина погрешности будет ≈ в середине интервала, а 0 – на концах интервала

На конце отрезка набл. Участвуют большое число N поэтому величина погрешности уменьшается к концу интервала.

в) Идеальный фильтр низких частот практически не существует.

Поэтому восстановление исходного сигнала осуществляется с погрешностью, которая зависит от порядка фильтра.

г) В теореме Котельникова в момент взятия отсчётов используются дельта импульсы.

Поэтому теорема ничего не говорит какую длительность надо использовать для дискретизации.

- Короткие импульсы расширяют спектр (-), но позволяют организовать многоканальную передачу.

- Широкие импульсы сужают спектр (+), но получаются одноканальные системы.

Кроме того, от длительности дискретизации импульсов зависит и погрешность восстановления исходных сигналов в приёме.

д) Апертурная погрешность

Она связана конечным временем одного преобразования и неопределённостью момента времени его окончания, т.е. вместо равномерной дискретизации на практике получаются неравномерная.

Величину этой погрешности можно оценить исходя из - опер. инт.

Для снижения опер. погрешности приходится увеличивать

частоту дискретизации.

Квантование сигналов по уровню.

Э та процедура преобразования непрерывного сигнала в последовательность дискретных значений с помощью нелинейного устройства (квантователь) ↔

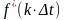
Точные значения заменяются приближёнными.

Ошибка

Ошибку можно оценить вычитая исходный и квантовый сигнал .

А точно восстановить исходный квантов. Нельзя т.к. каждому дискр. значению соответствует - шаг квантования

Чем меньше тем меньше ошибка

- среднеквадратичная ошибка (для равномерного кв-ния)

Если квантование неравномерное: наиболее вероятные значения с меньшим шагом, а наимен. вероят. с большим.

Квантование используется при аналогоцифровом преобразовании (АЦП) сигналов = дискр.+ ква-е. + кодиров.

Поскольку ошибка квантования считается помехой, то выр-т откланения

n – разрядность кода П – пик фактор сигнала.

П = 3 - для телефонии

Т.е. увеличение разрядности кода → возрастает соотношение с/ш

Для неравномерного квантования используют компандерные системы. Это система из 2х нелинейных преобразователей.

АЦП – параллельный (быстродействующий)

- последовательный (простой)

- комбинированный