38 Методы суммирования отдельных составляющих погрешности.

При суммировании частных погрешностей прежде всего необходимо среди них выделить систематические и случайные.

Погрености
Первичные	Частные
	Систематические	Случайные
Скалярная детерменированная	+ Δyqn	–
Скалярная случайная	+ – М(Δyqn)	+ S(Δyqn)
Векторная детерменированная	+ Δyqn	–
Векторная случайная	+ – М(Δyqn)	+ S(Δyqn)

Если погрешности систематические то их суммируют алгеброически, если случайные, то суммируют по правилам суммирования случайных величин.

К систематическим частным погрешностям приводят детерменированные первичные погрешности.

Суммарная погрешность от несоответствия параметров q_n номинальным значениям при условии Δq_n <<q_n имеет вид

В случаи случайных погрешностей раздельно суммируют мат. ожидание и СКО

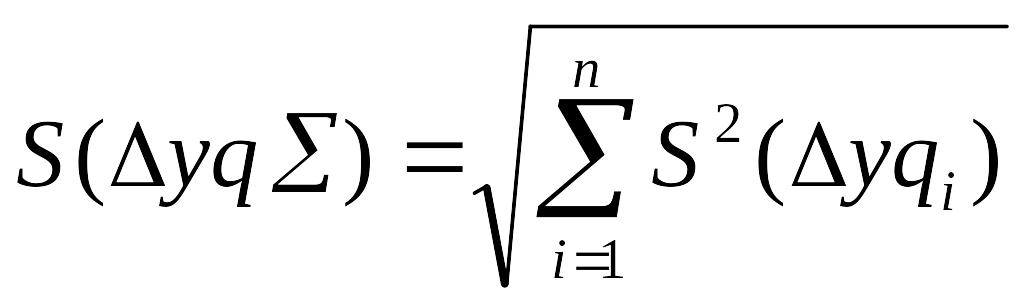
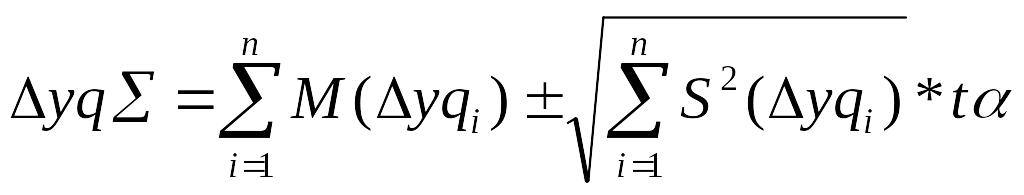
При точностном анализе в зависимости от применяемого метода, частные погрешности определяются и суммируются в соответствии со своей спецификой.

39 Методы анализа точности измерительных цепей: классификация методов, их сущность, теоретические основы.

Анализ точности измерительного устройства заключается в определении его результирующей погрешности на основании информации о номинальных значениях и характеристиках точности размеров и параметров отдельных деталей, элементов, узлов, блоков и т.п. 1) Метод максимума-минимума является достаточно простым, но дает несколько завышенный результат погрешности, т.к. при его реализации находится минимальное и максимальное значение погрешности устройства. Сущность подхода заключается в том, что в качестве первичных погрешностей используют максимально возможные отклонения значений параметров и размеров от их номинальных значений. Причем эти отклонения задаются в наиболее неблагоприятных комбинациях, поэтому все первичные погрешности принимаются за детерминированные, а все частные, соответственно, суммируются алгебраически. При реализации метода находят 2 предельных значения погрешности, которые соответствуют отклонениям внутренних параметров. При нахождении первого в качестве первичных погрешностей задается верхнее предельное отклонение всех параметров и размеров, у которых коэффициент влияния является положительным (увеличивающие параметры) и нижние предельные отклонения для параметров, у которых коэффициент влияния отрицательный (уменьшающие параметры). Второе значение погрешности определяется наоборот, когда для параметров с положительным коэффициентом влияния берутся нижние отклонения, а для параметров с отрицательным коэффициентом – верхние. Найденные два предельных значения погрешности определяют границы, в пределах которых может находиться значение погрешности устройства. Обобщенное выражение для определения максимального или минимального значений погрешности при учете N первичных погрешностей и M влияющих факторов имеет вид:

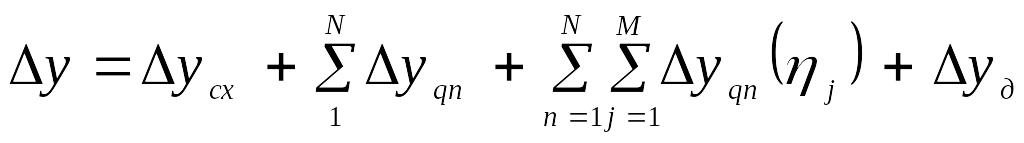
2) Метод вероятностного анализа. При реализации данного метода суммарная погрешность определяется из условия, что некоторые составляющие являются детерминированными, а некоторые случайными. Результирующая погрешность определяется как случайная величина, имеющая математическое ожидание (систематическую составляющую) и среднеквадратическое отклонение или дисперсию (случайную составляющую). Детерминированные, т.е. известные составляющие погрешности, складываются с мат. ожиданиями случайной составляющей погрешности и определяют общую систематическую составляющую погрешности. Случайные составляющие суммируются по правилам суммирования случайных величин - находится среднеквадратическое значение суммарной составляющей погрешности, по которому рассчитывают размер доверительного интервала (с учетом вида закона распределения суммарной погрешности). Результат такого расчета в виде доверительного интервала позволяет оценить ожидаемое значение погрешности с принятой доверительной вероятностью, отличной от единицы. Выражение для суммарной погрешности при наличии детерминированных и случайных первичных погрешностей можно обобщенно представить в виде:

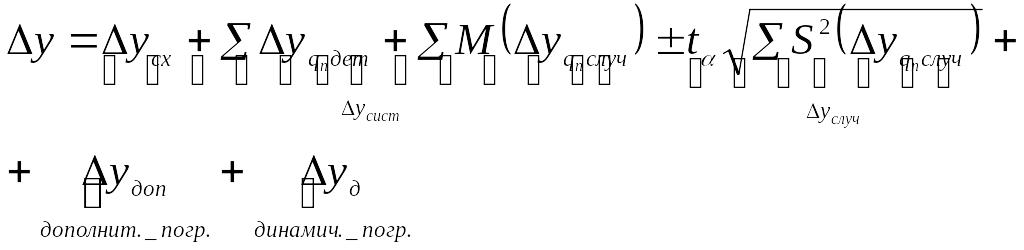
3) Метод ситуационного моделирования учитывает дефицит априорной информации. Суть метода состоит в том, что законы мат. статистики применяют для неслучайных величин, и при этом принимается ряд допущений и упрощений. Для реализации метода вводятся параметры, аналогичные соответствующим параметрам для случайных величин: - координата середины поля допуска внутреннего параметра принимается за математическое ожидание первичной погрешности: М*(∆q) = Е₀; - поле допуска принимают за доверительный интервал Е*: Т₁=Е*; - вместо квантиля распределения t_p вводят некоторое значение коэффициента k, которое выбирают по договоренности любым числом (t_p = k); - аналог среднеквадратического отклонения определяют из выражения: S*(∆q) = Т₁/k.

Частные погрешности определяются:

Расчеты погрешности производят по алгоритму вероятностного анализа, определяя аналог доверительного интервала суммарной погрешности путем умножения ее СКО на ранее выбранное значение k. ∆yq_n=M’(∆yq_n)±k*U(∆yq_n).